Ответы
Объяснение:
1.
r=D:2=1:2=0,5 дм
ответ: Б
2.
ответ: А
3.
ответ: Б
4.
ответ: А
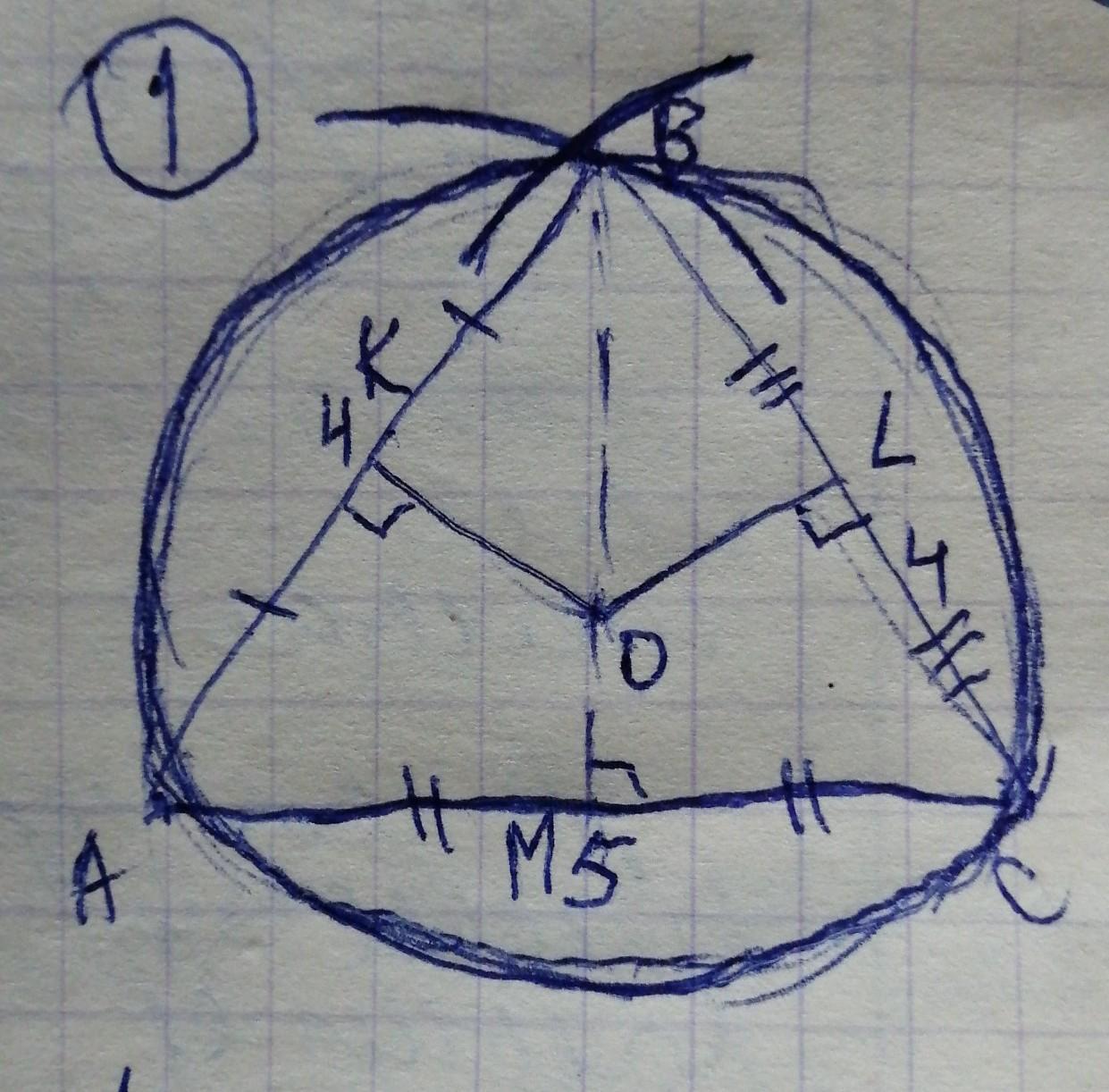
1.на фото 1
1. чертим отрезок АС=5 см
проводим дугу с центром А и радиусом 4 см
проводим дугу с центром С и радиусом 4 см.
на пересечении дуг получаем точку В .
∆АВС - равнобедреный (АВ=ВС=4 см).
чертим серединный перпендикуляр ВМ к стороне АС
чертим серединный перпендикуляр ОК к стороне АВ
чертим серединный перпендикуляр ОL к стороне ВС
на пересечении серединных перпендикуляров получаем центр описанной окружности около равнобедренного треугольника.
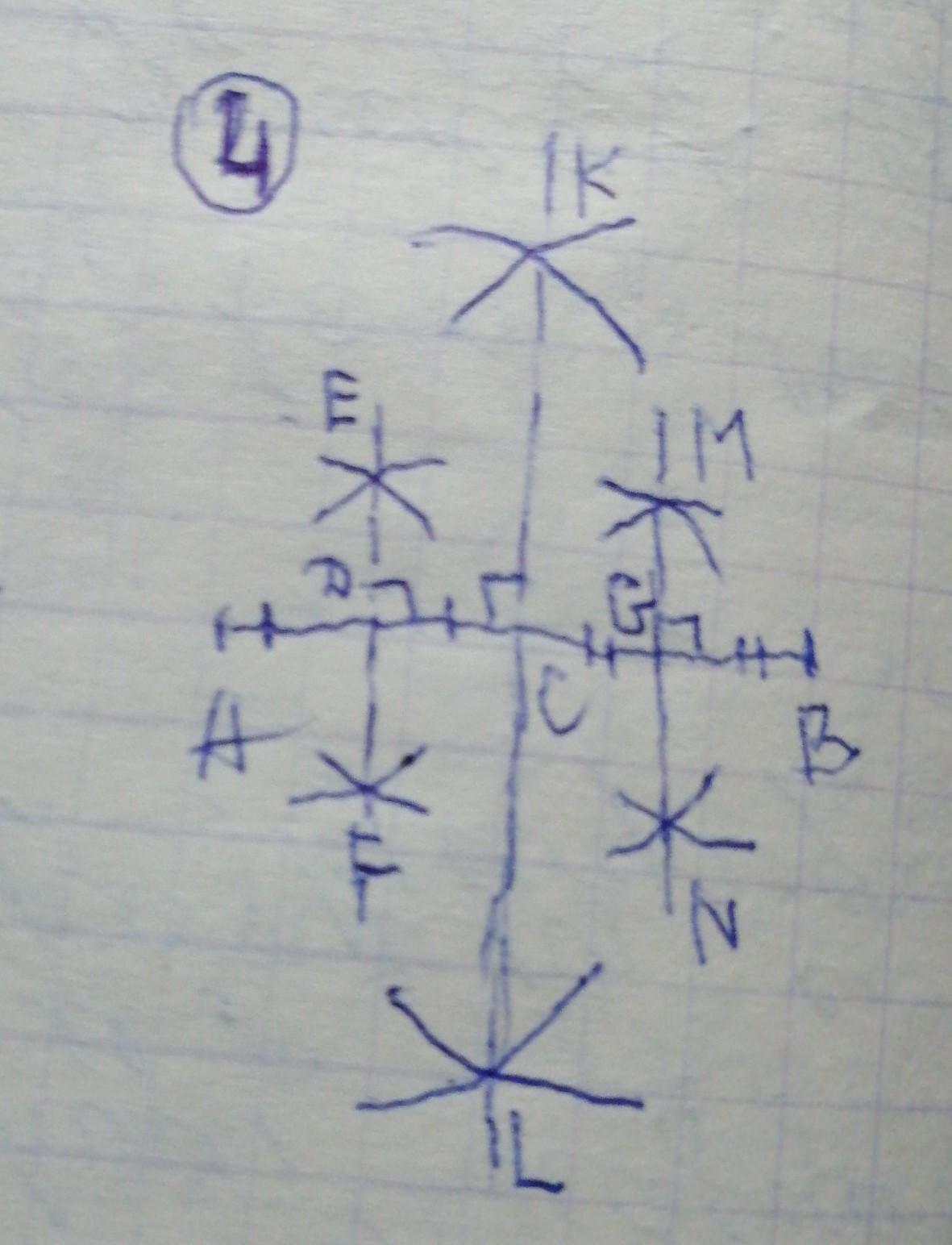
2.на фото 4
для того ,чтобы поделить отрезок на 4 равные части чертим серединные перпендикуляры .
чертим при помощи линейки отрезок АВ.
циркулем чертим дуги с центром А и с центром В и радиусом больше середины АВ .
на пересечении дуг получаем точки К и L ,соединяем КL .
на пересечении АВ и КL получаем точку С ,которая является серединой АВ.
для нахождения середины АС чертим дуги с центром А и с центром С и произвольным радиусом больше середины АС.
на пересечении получаем точки Е и F.
соединяем ЕF.
на пересечении АС и ЕF получаем точку D ,которая является серединой АС.
Анолочично получаем точку G ,которая является серединой СВ.
Всё ,отрезок разделили на 4 равные части.
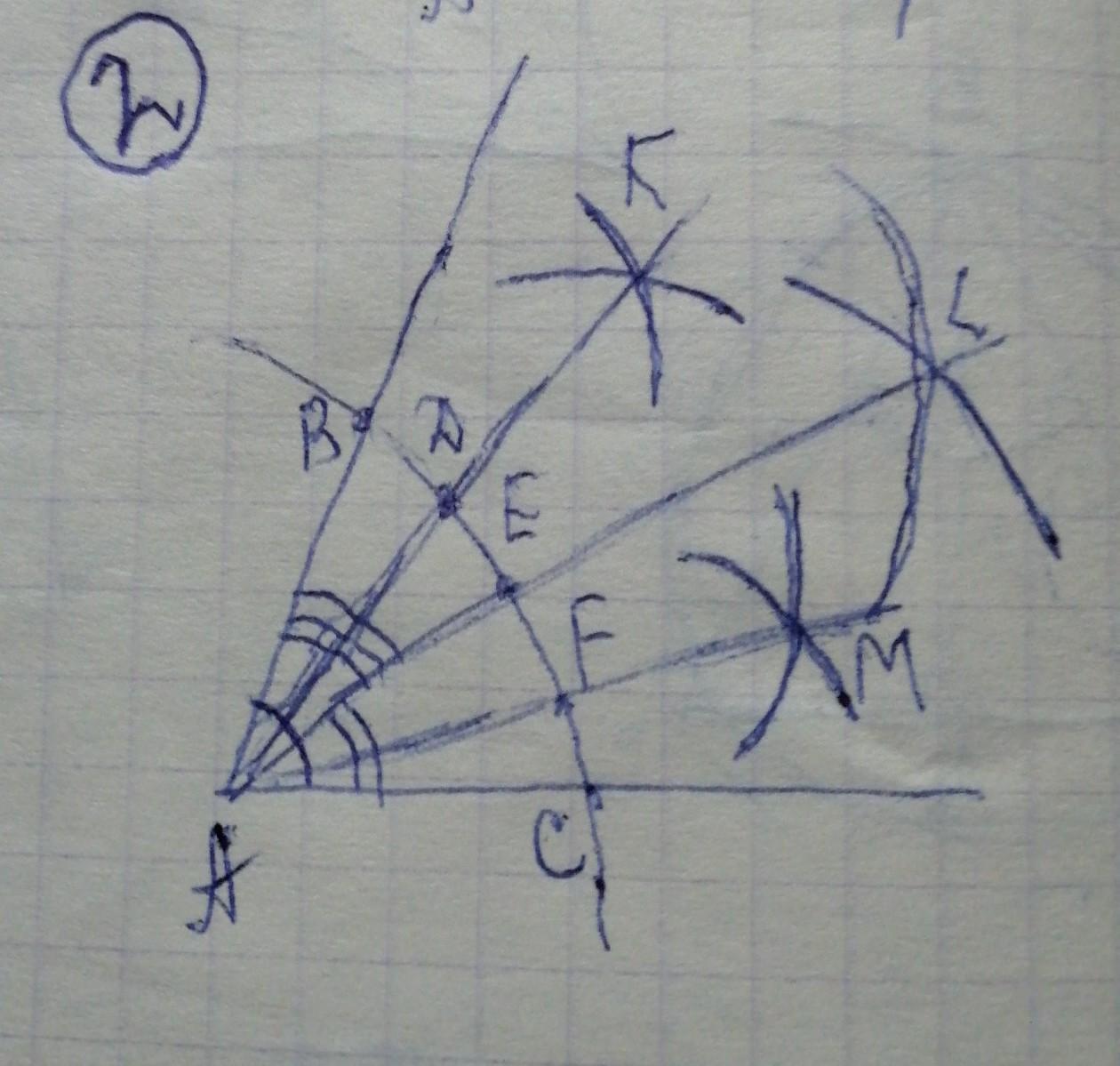
3. на фото 2
чтобы разделить угол на равные части чертим биссектрисы углов.
чертим исходный угол при помощи линейки.
Чертим дугу с центром А и произвольным радиусом.
на пересечении сторон и дуги получаем точки В и С .
Чертим дугу с центром В и произвольным радиусом.
чертим дугу с центром С и тем же радиусом.
на пересечении дуг получаем точку L.
AL - биссектриса ∠ВАС
чертим дугу с центром В и произвольным радиусом.
чертим дугу с центром Е и тем же радиусом .
на пересечении дуг получаем точку К.
АК - биссектриса ∠ВАЕ.
чертим дугу с центром С и произвольным радиусом.
чертим дугу с центром Е и тем же радиусом.
на пересечении дуг получаем точку М.
АМ - биссектриса ∠САЕ
Получили 4 равных угла .
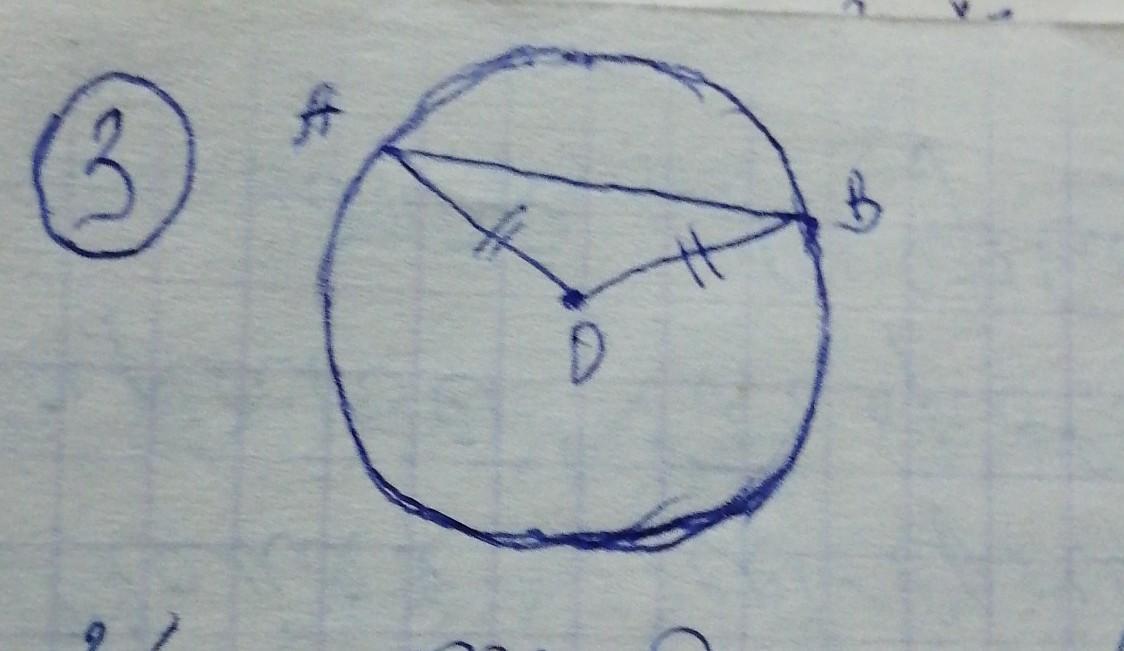
4. на фото 3
∆АВС - равнобедреный,т.к АО=ОВ - как радиусы.
В равнобдренном треугольнике боковые стороны равны.