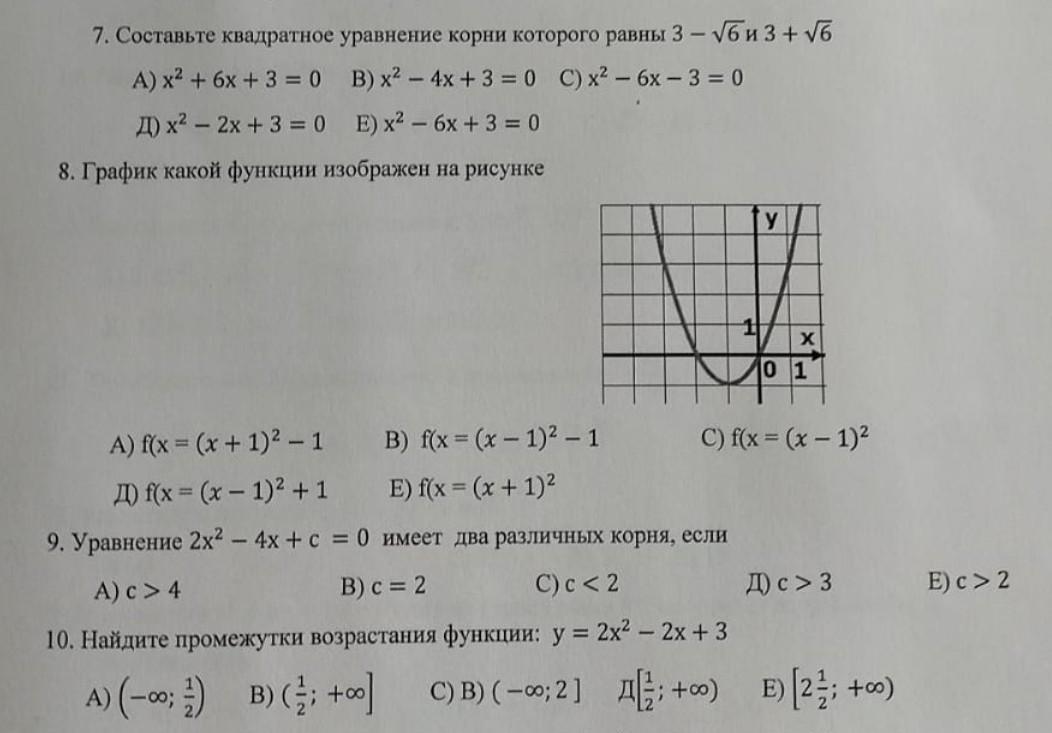
7. Составьте квадратное уравнение корни которого равны 3-√6 и 3 +√6 A) x2 + 6x + 3 = 0 B) x² - 4x + 3 = 0 C) x² - 6x-3=0 Д) x² - 2x + 3 = 0 E) x² - 6x + 3 = 0 8. График какой функции изображен на рисунке B) f(x = (x - 1)2 – 1 E) f(x = (x + 1)2 y x 10 1 c) f(x = (x - 1)2 A) f(x = (x + 1)2 – 1 Д) f(x = (x - 1)2 + 1 9. Уравнение 2х2 - 4х + c = 0 имеет два различных корня, если A)c> 4 B) c = 2 C) c < 2 10. Найдите промежутки возрастания функции: у = 2x² - 2x + 3 A) (-∞; ;) B) (;; +∞0] С)B)(-∞;2] Д; +∞o) E) (23; +∞) Д) с > 3 E) c > 2
Приложения:
Ответы
Ответ дал:
0
Ответ:
7) Корни квадратного уравнения равны .
Тогда сумма корней равна , a
произведение корней равно .
Квадратное уравнение имеет вид . (E)
8) На рисунке график функции . (A)
9) Уравнение имеет два различных корня , если
. (C)
10) , ветви вверх
Вершина параболы имеет абсциссу, равную
Промежуток возрастания . (Д)
Приложения:

Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад