Найдите сумму длин вписанной и описанной окружностей правильного треугольника со стороной 6√3.С подробным решением и рисунком.
Ответы
Ответ дал:
1
Ответ: 18π см. 56,52 см.
Объяснение:
Сторона треугольника а= 6√3 см
R описанной окружности R= a/√3 = (6√3)/√3 = 6 см.
r вписанной r=a√3/6 = (6√3*√3)/6 = 3 см.
(См. скриншот).
Длина окружности C=2πR и c=2πr. Тогда
С+с = 2πR+2πr = 2π(R+r) =2*π(6+3) = 18π см. =>
или
С+с=2*3,14*9=6.28*9 = 56,52 см.
Приложения:
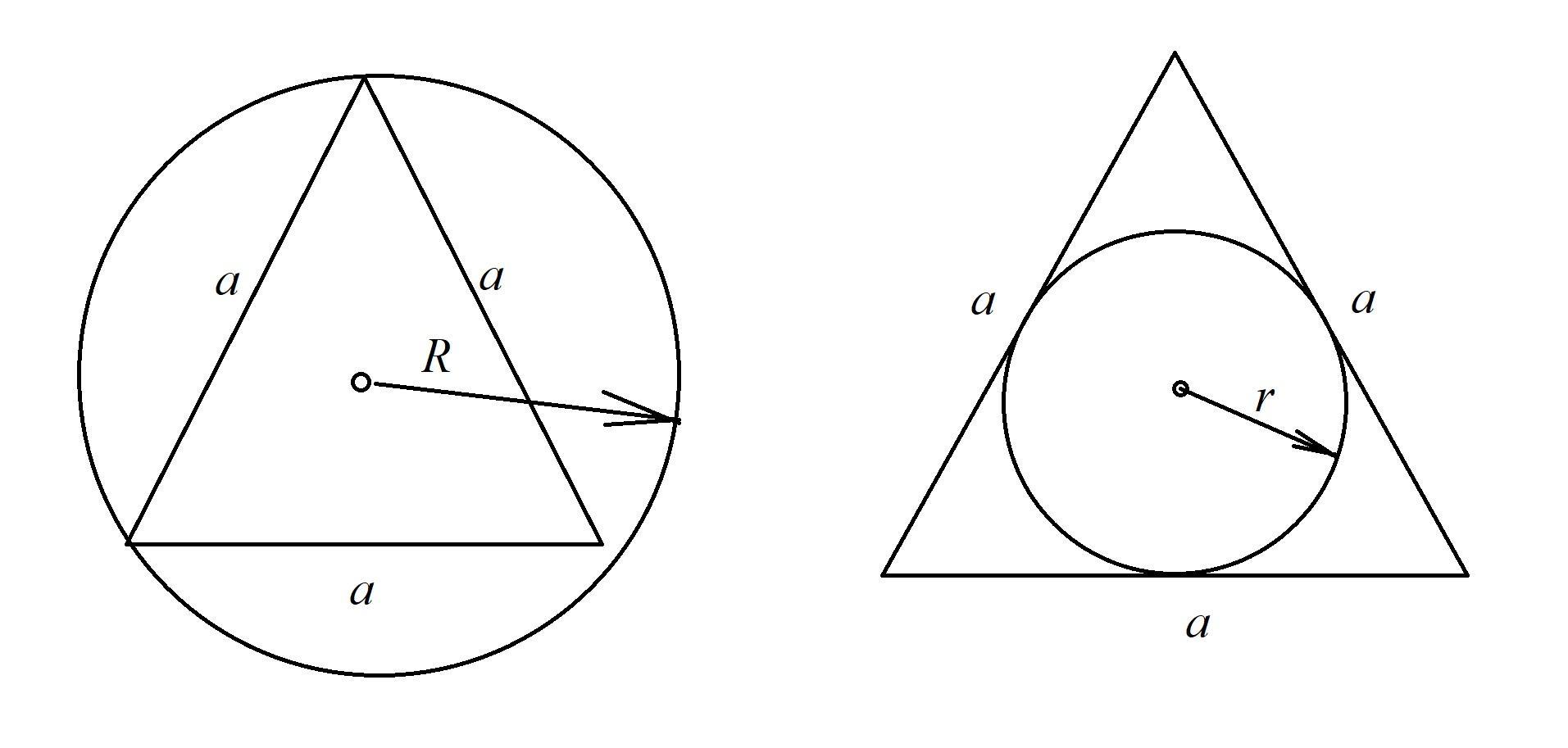
whysol:
в общем говоря сумма составляет 56,52,если использовать формулу длиы окружности и суммировать,да?
Извините,если затрудняю вас,но вы нем могли бы,пожалуйста,решить и другие задачи?
Вас заинтересует
1 год назад
1 год назад
3 года назад
3 года назад