Question

Найдите радиус окружности,вписанной в треугольник со сторонами 20,20 и 24 см.С подробным решением и рисунком.​

Answer 1

Ответ:

Радиус вписанной окружности равен 6см

Объяснение:

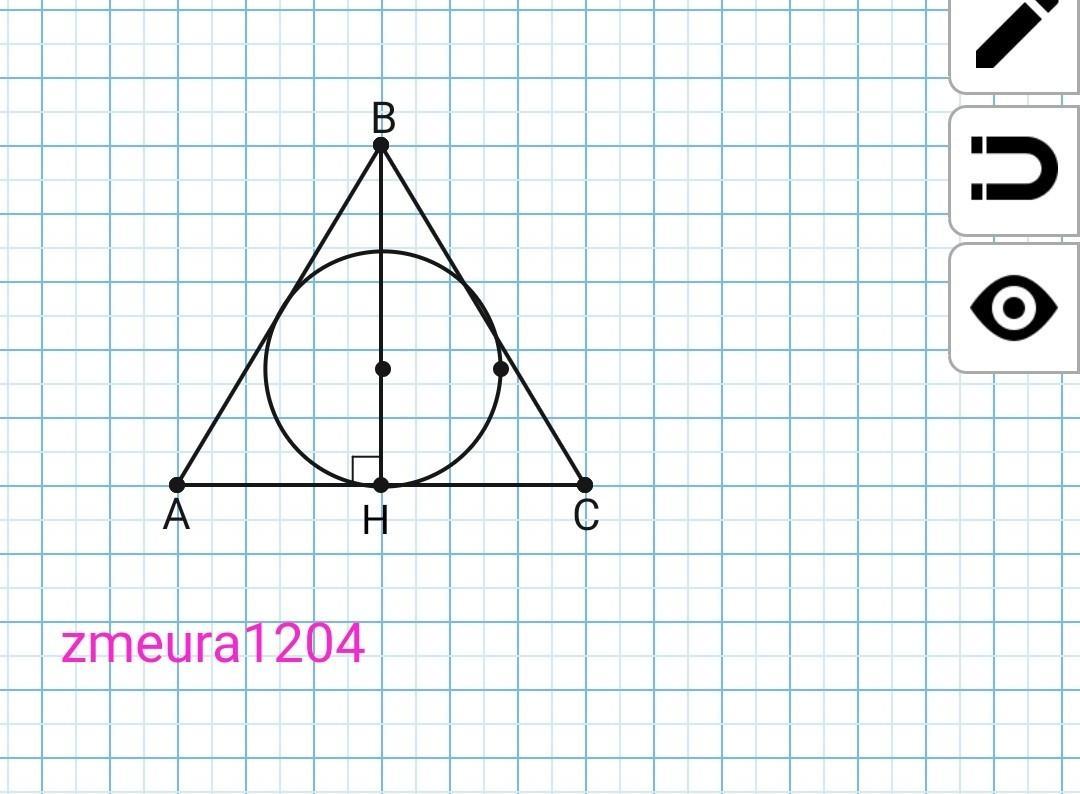
∆АВС

AB=BC=20см

АС=24см

r=?

Решение:

ВН- высота, медиана равностороннего треугольника

АН=АС/2=24/2=12 см.

∆ABH- прямоугольный треугольник

Теорема Пифагора:

ВН=√(АВ²-АН²)=√(20²-12²)=

=√(400-144)=√256=16см

S(∆ABC)=½*AC*BH=

=½*16*24=192см²

р=(АВ+ВС+АС)/2=(20+20+24)/2=

=64/2=32см

r=S(∆ABC)/p=192/32=6см