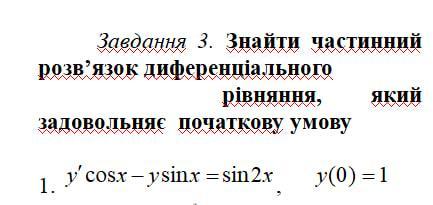Ответы
Ответ дал:
0
Ответ:
Найти частное решение линейного дифференциального уравнения 1-го порядка .
Cделаем замену :
Частное решение : ,
.
Приложения:
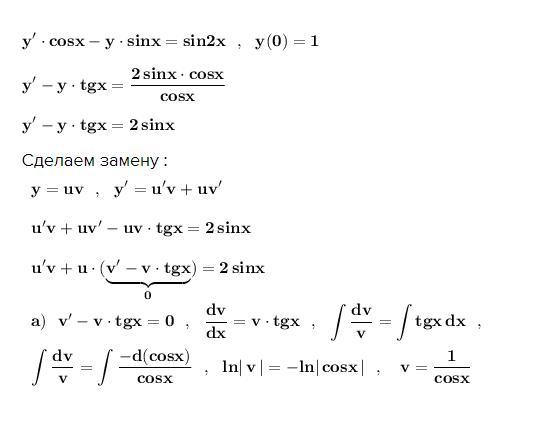
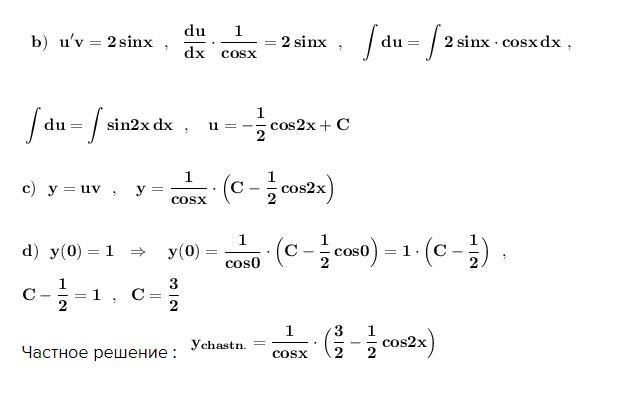
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад