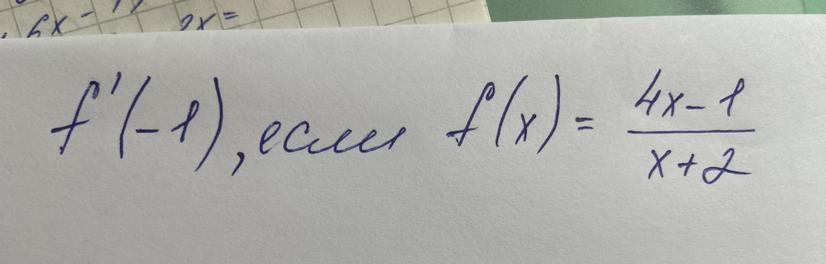Ответы
Ответ дал:
1
Пошаговое объяснение:
Используем правило дифференцирования частного и производную композиции функций:
f’(x)=[(4x-1)’(x+2)-(4x-1)(x+2)’]/(x+2)^2
f’(x)=(4(x+2)+(4x-1)(1))/((x+2)^2)
f’(x)=(8x+7)/((x+2)^2)
Теперь можем найти f’(-1):
f’(-1)=(8*(-1)+7)/((-1+2)^2)
f’(-1)=(-1)/1
f’(-1)=-1
julsi32:
Извините, а как получилось в 3 строчке: (8х+7)? У меня почему-то получилось 9/(х+2)^2
Извините, это моя ошибка. В правильном решении третьей строки должно быть:
f’(x)=(8x-9)/((x+2)^2)
Таким образом, значение f’(-1) будет:
f’(-1)=(8*(-1)-9)/((-1+2)^2) = -17.
f’(x)=(8x-9)/((x+2)^2)
Таким образом, значение f’(-1) будет:
f’(-1)=(8*(-1)-9)/((-1+2)^2) = -17.
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад