В равнобедренном треугольнике один из внешних углов равен 60 гр.,а высота, проведенная к боковой стороне, равна 17 см.Найдите основание треугольника.
Приложения:

Ответы
Ответ дал:
1
Ответ:
34 см
Объяснение:
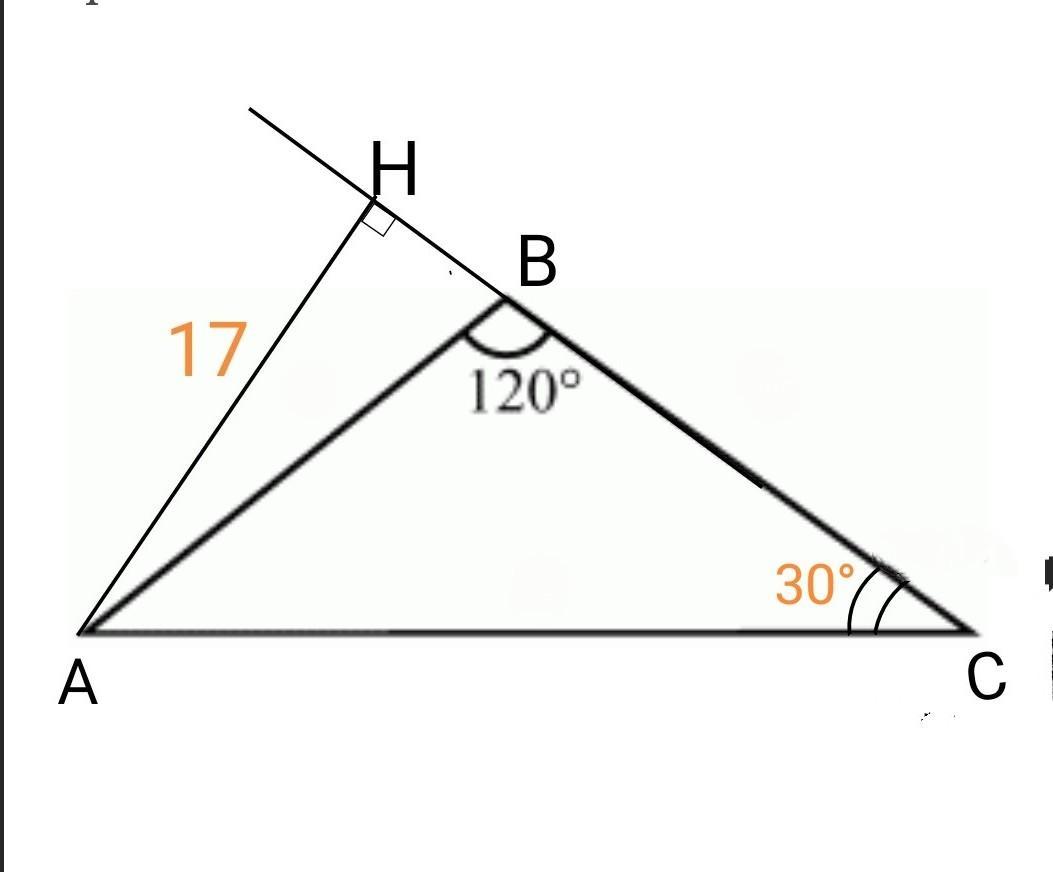
1. Пусть дан равнобедренный треугольник АВС с основанием АС.
Данный внешний угол острый, значит смежный с ним внутренний - тупой. Таким может быть. только угол В при вершине. (В противном случае два равных угла при основании были бы тупыми, а это противоречит теореме о сумме углов треугольника).
Итак, ∠ В = 120°, высота АН, проведённая к боковой стороне ВС, равна 17 см
2. Углы при основании равнобедренного треугольника равны по теореме, по теореме о сумме углов треугольника каждый из них по
∠С = ∠А = (180° - 120°) : 2 = 30°.
3. В прямоугольном ∆АНС ∠С = 30°, тогда лежащий напротив пакет АН = 1/2•АС, АС = 2 • 17 = 34 (см).
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад