Question

4. Знайдіть площу трапеції, основи якої дорівнюють 13см та 52см, а бічні сторони 41см та 50см. 5 таап утмокутного трикутника​

Answer 1

Ответ:

Площа трапеції дорівнює 1300 см²

Объяснение:

Знайдіть площу трапеції, основи якої дорівнюють 13 см та 52 см, а бічні сторони 41 см та 50 см.

Розв'язування

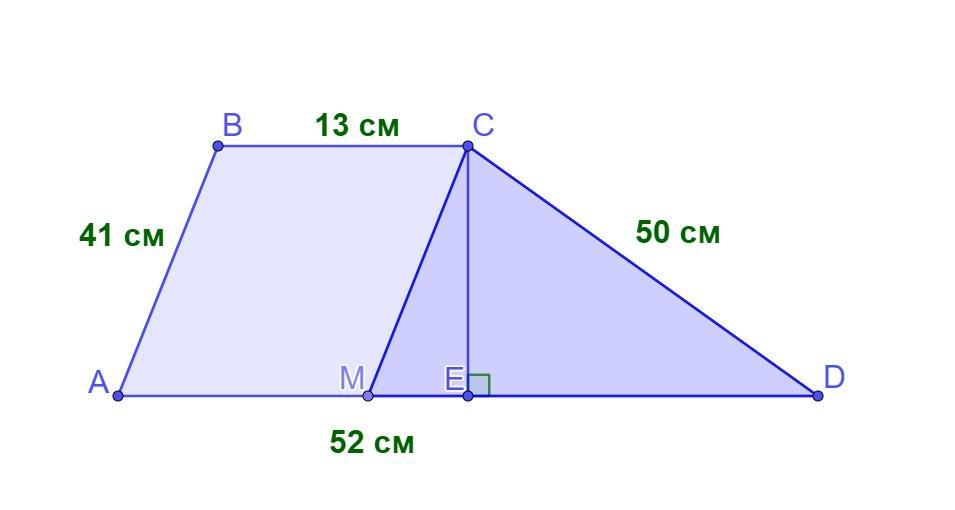
Нехай ABCD - дана трапеція, BC ║AD, АВ = 41 см, ВС = 13 см, CD = 50 cм, AD = 52 см.

1) Проведемо СМ ║ АВ. Отримаємо паралелограм АВСМ.

За властивістю паралелограма:

СМ = АВ = 41 см

АМ = ВС = 13 см

За аксиомою вимірювання відрізків маємо:

MD = AD - AM = 52 - 13 = 39 (см).

2) Знайдемо висоту СЕ у ΔMCD.

S(ΔMCD) = 1/2 · MD · CE

Тоді:

$CE = \dfrac{2S_{MCD}}{MD}$

За формулою Герона:

$S_{MCD}=\sqrt{p(p-MC)(p-CD)(p-MD)}$

де р - полупериметр ΔMCD.

$p=\dfrac{MC+CD+MD}{2}=\dfrac{41+50+39}{2} =\dfrac{130}{2} =\bf 65$  (см)

$S_{MCD}=\sqrt{65(65-41)(65-50)(65-39)} =\\\\=\sqrt{65\cdot 24\cdot 15\cdot 26}=\sqrt{5\cdot13\cdot3\cdot 2\cdot 4\cdot 5\cdot 3\cdot2 \cdot13} =\\\\=5\cdot13\cdot3\cdot2\cdot2=780$(см²)

$CE = \dfrac{2\cdot 780}{39} =\bf 40$  (см)

3) СЕ  є також висотою трапеції ABCD .

Отже:

$S_{ABCD}=\dfrac{BC+AD}{2} \cdot CE = \dfrac{13+52}{2} \cdot40=65\cdot20=\bf 1300$  (см²)

Відповідь: 1300 см²

$SPJ1