Question

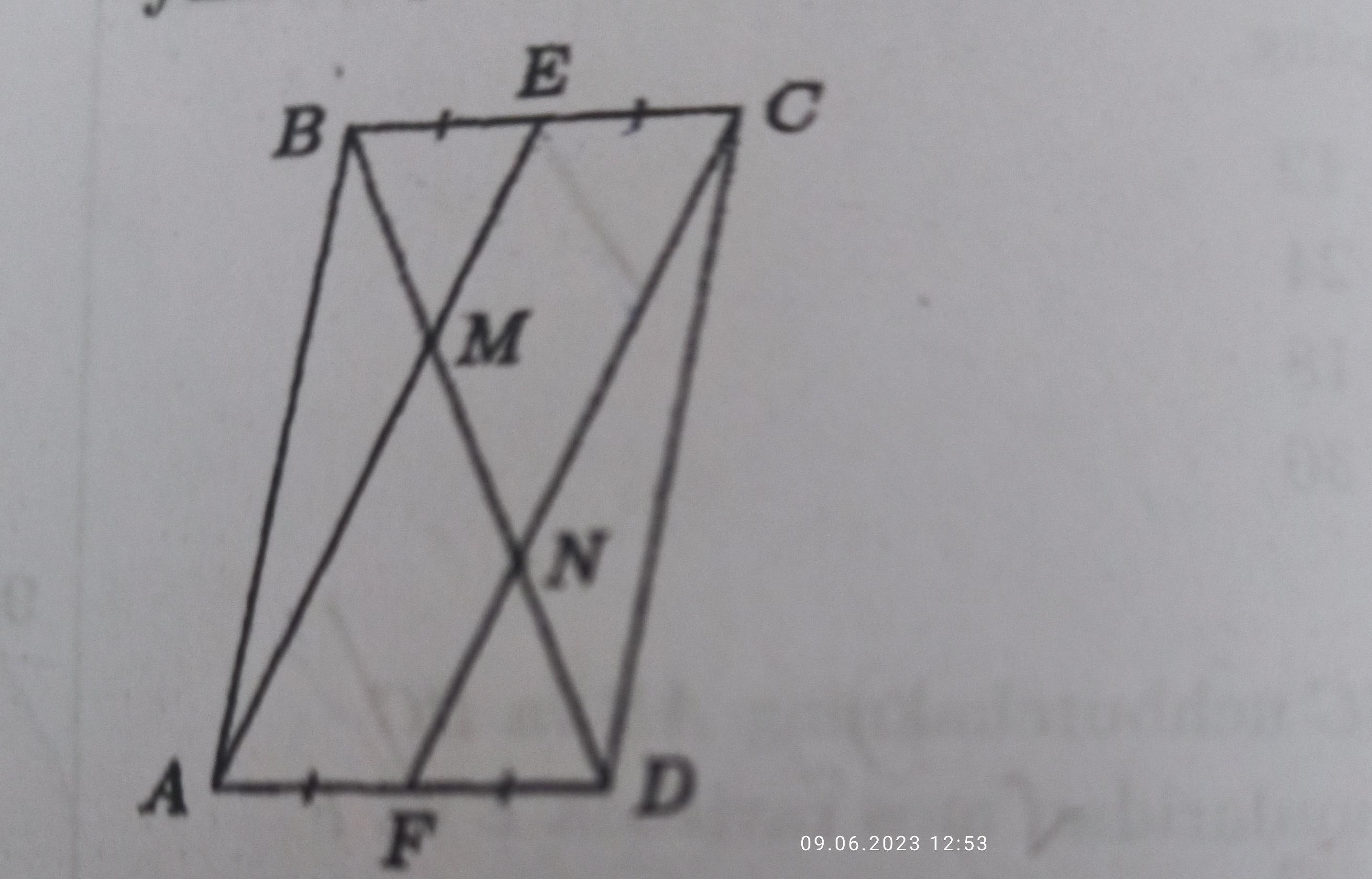
На рисунке изображена параллелограмм ABCD. Проведены отрезки CF и AE которые делят стороны AD и BC на равные отрезки. Если площадь параллелограмма равна 72 , то найдите площадь треугольника BEM.


Помогите пожалуйста. Дам 50 баллов!!!

Answer 1

Ответ:

Площадь треугольника ВЕМ равна 6 ед.².

Объяснение:

На рисунке изображена параллелограмм ABCD. Проведены отрезки CF и AE которые делят стороны AD и BC на равные отрезки. Если площадь параллелограмма равна 72 , то найдите площадь треугольника BEM.

Дано: ABCD - параллелограмм;

ВЕ = ЕС; AF = FD;

S(ABCD) = 72.

Найти: S(BEM)

Решение:

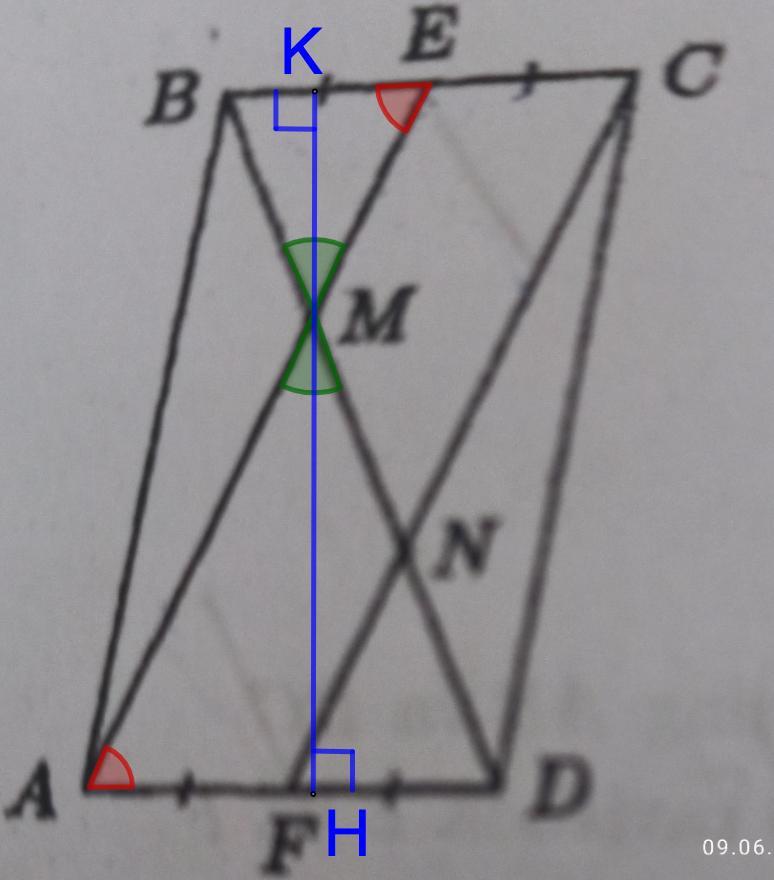
Через точку М проведем КН ⊥ AD.

• Противоположные стороны параллелограмма равны.

⇒ ВС = AD

Пусть ВС = AD = 2a

⇒ BE = EC = AF = FD = a

• Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне.

⇒ S(ABCD) = AD · KH

72 = 2a · KH   ⇒   KH = 36/a

Рассмотрим ΔMBE и ΔMDA.

∠BME = ∠DMA (вертикальные)

∠МЕВ = ∠МАD (накрест лежащие при BC || AD и секущей АЕ)

⇒ ΔMBE ~ ΔMDA (по двум углам)

• Отношение высот подобных треугольников, проведенных к сходственным сторонам, равно коэффициенту подобия.

$\displaystyle \frac{MK}{MH}=\frac{BE}{AD}=\frac{a}{2a}=\frac{1}{2}=k$

Пусть MK = х, тогда МН = 2х   ⇒ КН = 3х.

$\displaystyle 3x=\frac{36}{a}\;\;\;|:3\\ \\x = \frac{12}{a}$

⇒ MK = 12/a

Найдем площадь ΔВЕМ.

• Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне.

$\displaystyle S(BEM)=\frac{1}{2}BE \cdot MK=\frac{1}{2}\cdot a\cdot \frac{12}{a}=6$

Площадь треугольника ВЕМ равна 6 ед.².

#SPJ1