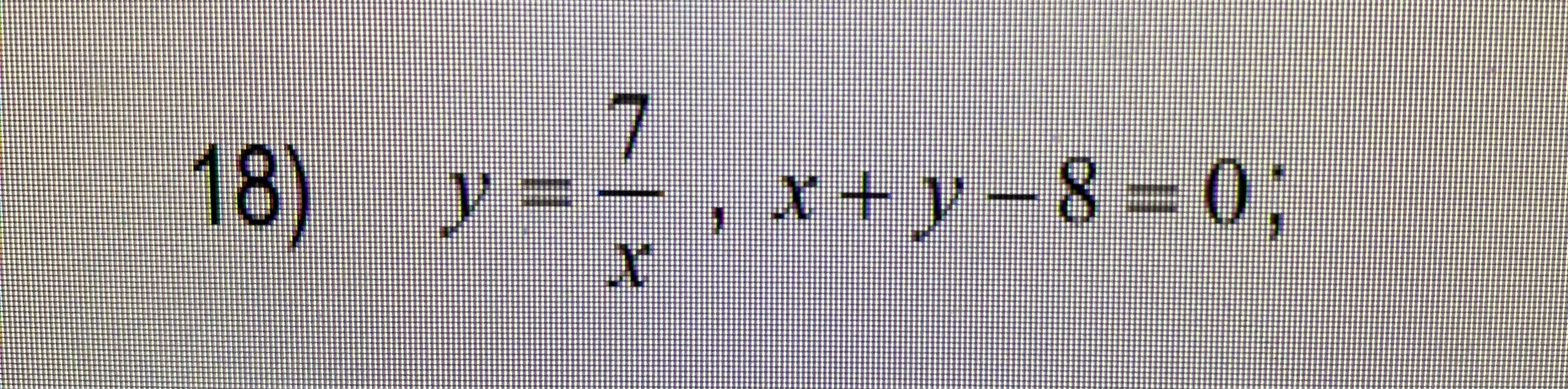Question

Обчислити площу фігури ,обмежену кривими

Answer 1

Ответ:      10,379  кв.ед.

Пошаговое объяснение:

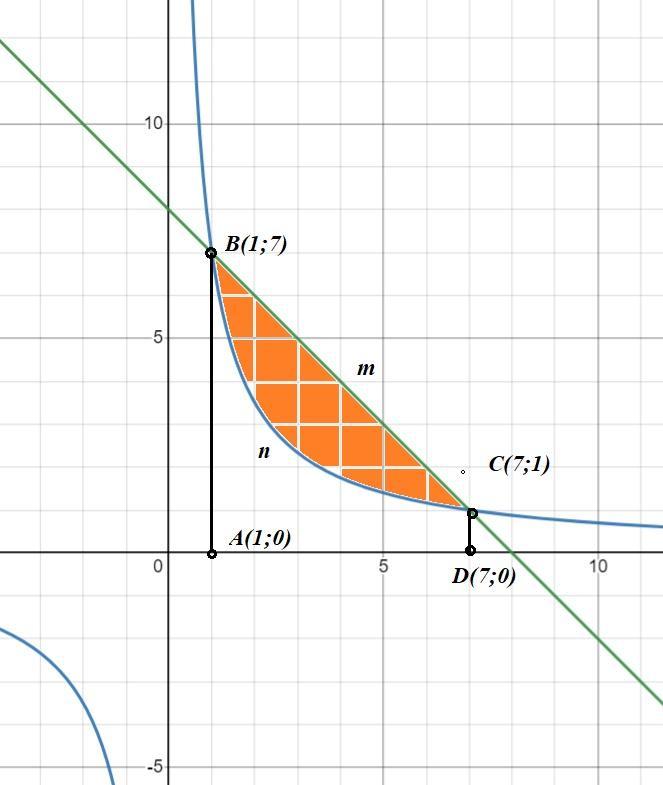
Строим графики функций   y=7/x  и   x+y-8=0 => y=8-x; (См. скриншот)

S=s(ABmCD)=s(ABnCD).

s=∫ₐᵇf(x)dx.

По формуле Ньютона-Лейбница

∫ₐᵇf(x)dx = F(x)|ₐᵇ = F(b) - F(a).

По графику определяем пределы интегрирования a=1;  b=7.

Проверим,  решив систему

7/x = 8-x.

x1=a=1;  x2=b=7.  Тогда

S=∫₁⁷(8-x)dx - ∫₁⁷(7/x)dx = 24 - 13.621 = 10,379  кв.ед.

1)  ∫₁⁷(8-x)dx = ∫₁⁷8dx -∫₁⁷xdx = 8(x)|₁⁷ - 1/2(x²)|₁⁷ = 8(7-1) - 1/2(7²-1²) =

= 48 - 1/2(48) = 48-24 = 24 кв.ед.

2)  ∫₁⁷(7/x)dx  = 7*ln(x)|₁⁷ = 7(ln7 - ln1) = 7*(ln7) = 13.621 кв.ед.