Ответы
Ответ дал:
1
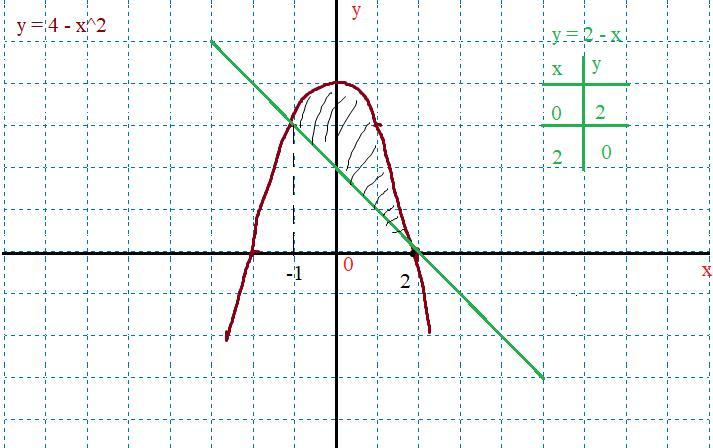
По графику найдем точки пересечения данных функций.
Точки пересечения: х1 = -1, х2 = 2
Искомая фигура находится между графиками. Найдем ее площадь через интегралы:
Ответ: 4,5 кв ед
PS Если что, графики строил по преобразованию
Приложения:
KardelSharpbrain:
и в значении интегралов не 1 а -1. Я не разобрался, как там поставить значение отрицательное, число влезало в в основную формулу а минус оставался
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад
