Ответы
Ответ дал:
2
Ответ:
Циркуляция векторного поля:
Пошаговое объяснение:
- векторное поле
По формуле Стокса в общем виде:
Ротор векторного поля:
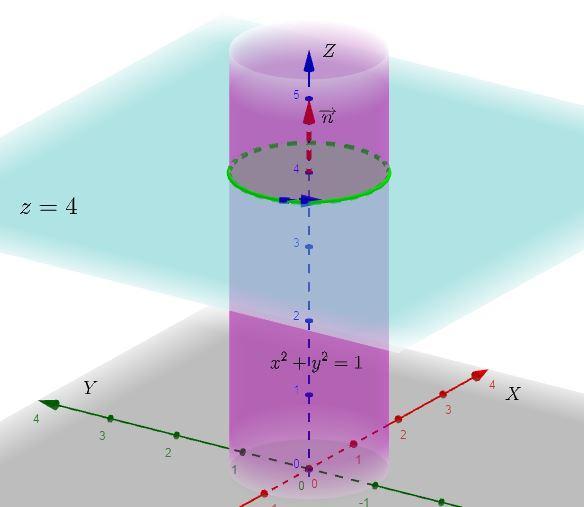
Вектор нормали к поверхности
, где
площадь ограниченная контуром
.
Так как контур ограничивает окружность радиуса
, то площадь поверхности можно найти по формуле площади круга, тогда:
#SPJ1
Приложения:
avval666:
Как вы используете такой шрифт?
Вас заинтересует
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад
