СРОЧНО С РИСУНКОМ
Найдите радиус описанной около прямоугольного треугольника окружности катеты которого равны 12 и 9
Ответы
Ответ дал:
1
Відповідь: R = 7,5 см .
Пояснення:
У прямок. ΔАВС ∠С = 90° , а = 12 см , b = 9 см .
Як відомо центр кола , описаного навколо прямок. тр - ника ,
лежить на середині гіпотенузи .
АВ = с = √( a² + b² ) = √( 12² + 9² ) = √225 = 15 ( см ) ; с = 15 см , тому
R = 1/2 c = 1/2 * 15 = 7,5 ( см ) ; радіус описаного кола R = 7,5 см .
Ответ дал:
0
Ответ:
7,5 см.
Объяснение:
Радиус описанной около прямоугольного треугольника окружности равен половине гипотенузы.
Гипотенуза равна 15 см, т.к. это египетский треугольник с соотношением сторон 3:4:5.
Радиус R=15:2=7,5 см.
Приложения:
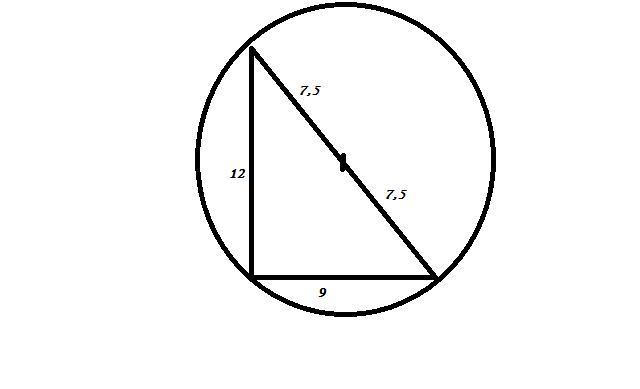
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад