Question

Надо подробно решить срочно

Answer 1

Ответ:

..................

Объяснение:

......... ..............

Answer 2

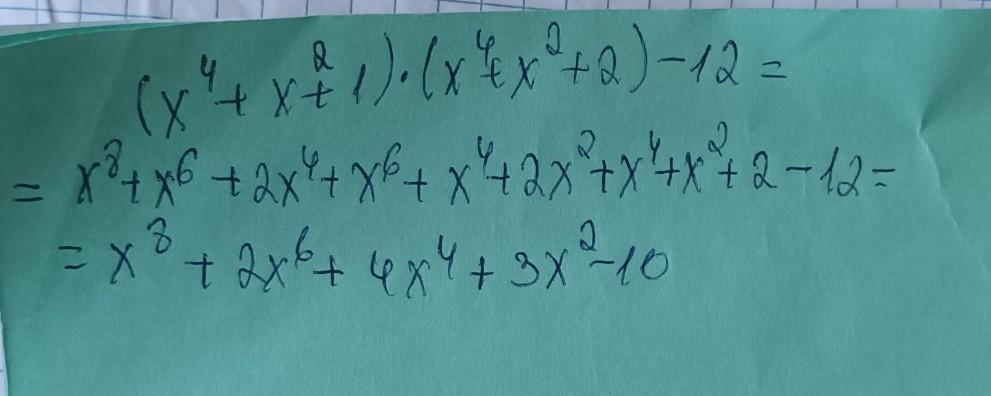
Відповідь:    А )  4 .

Пояснення:

   Зробимо заміну  t = x⁴ + x² + 1 , тоді даний вираз матиме вигляд

 ( x⁴ + x² + 1 )( x⁴ + x² + 2 ) - 12 = t( t + 1 ) - 12 = t² + t - 12 = ( t + 4 )( t - 3 )= 0 ;

   1)  t₁ = - 4 ;                                            2) t₂ = 3 ;

   x⁴ + x² + 1 = - 4 ;                                    x⁴ + x² + 1 = 3 ;

   x⁴ + x² + 5 = 0 ;                                     x⁴ + x² - 2 = 0 ;

   в обох біквадратних рівняннях зробимо заміну u = x² , ( u ≥ 0 ) :

   u² + u + 5 = 0 ;                                      u² + u - 2 = 0 ;    

D = - 19 < 0 , тому  uЄ ∅ ;                  D = 9 > 0 ; u₁ = - 2 < 0 ;  u₂ = 1  ;              

                                                            повернемося до змінної  х :

                                                            x² = 1 ;   x = ± √ 1 = ± 1  .

  Отже , даний початковий вираз розкладається на чотири

  множники з раціональними коефіцієнтами , а саме :

  ( x⁴ + x² + 1 )( x⁴ + x² + 2 ) - 12 = ( x⁴ + x² + 5 )( х² + 2 )( х + 1 )( х - 1 ) .