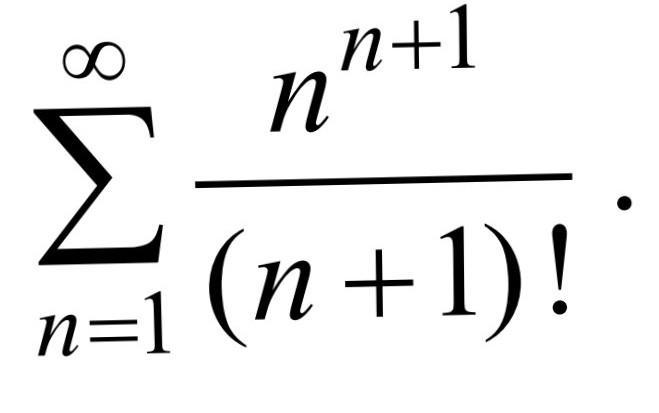Question

Помогите пожалуйста решить ​

Answer 1

Ответ:

Задан знакоположительный ряд     $\bf \sum \limits _{n=1}^{\infty }\, \dfrac{n^{n+1}}{(n+1)!}$     .

Применим достаточный признак Даламбера для определения сходимости ряда .

$\bf \lim\limits_{n \to \infty}\, \dfrac{a_{n+1}}{a_{n}}= \lim\limits_{n \to \infty}\, \dfrac{(n+1)^{n+2}}{(n+2)!}:\dfrac{n^{n+1}}{(n+1)!}=\\\\\\=\lim\limits_{n \to \infty}\, \dfrac{(n+1)^{n}\cdot (n+1)^2\cdot (n+1)!}{(n+1)!\cdot (n+2)\cdot n^{n}\cdot n}=\lim\limits_{n \to \infty}\, \dfrac{(n+1)^2}{(n+2)\cdot n}\cdot \underbrace{\bf \Big(1+\dfrac{1}{n}\Big)^{n}}_{\to \ e}=\\\\\\=\lim\limits_{n \to \infty }\, \underbrace{\bf \dfrac{n^2+2n+1}{n^2+2n}}_{\to \ 1}\cdot \ e=1\cdot e=e\approx 2,718281828459045 > 1$  

Так как предел  > 1 , то ряд расходится .