Question

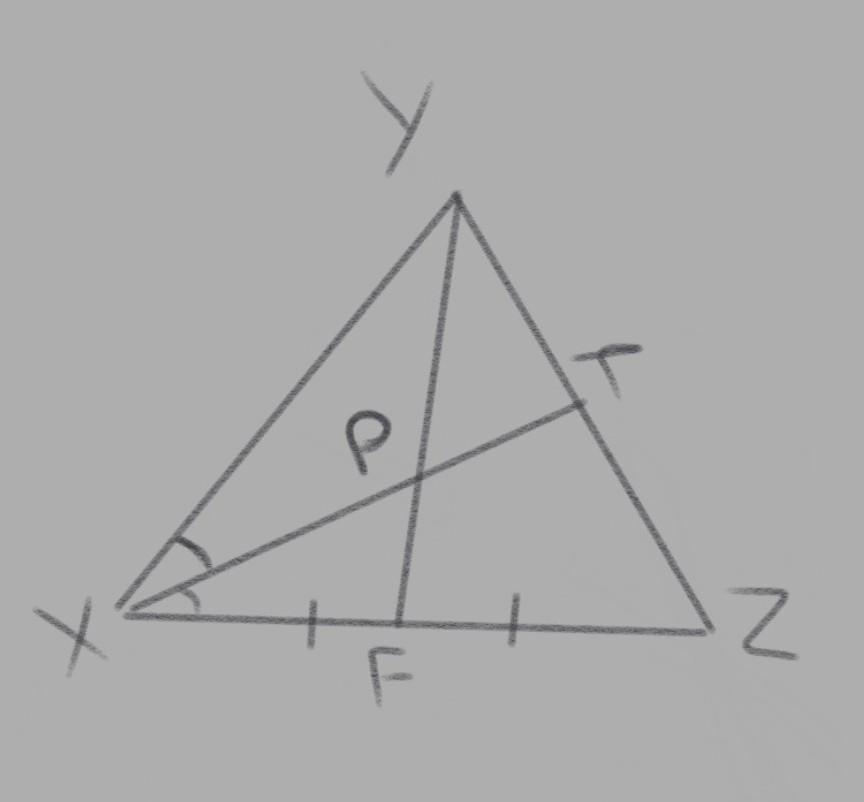
Дан треугольник XYZ, в котором YF - это медиана а XT - биссектриса. YF и XT пересекаютса в точке P. Определите, как относится площадь треугольника XPF к площади треугольника XYZ, если известно, что отношение длины стороны XY к длине стороны XZ равно 10/7

Answer 1

Ответ:

$\frac{54}{7}$

Объяснение:

Пусть XY=z, XZ=y, YT=x1, TZ=x2, YZ=x, XP=p1, PT=p2, XT=p

По свойству биссектрисы:

$\frac{x_1}{z} = \frac{x_2}{y} \\ \frac{z}{y} = \frac{x_1}{x_2} = \frac{10}{7}$

По теореме менелая, для треугольника XZT и прямой FY:

$1*\frac{p_1}{p_2} * \frac{x_1}{x} = 1 \\ \frac{p_1}{p_2} * \frac{ \frac{10}{7} x_2}{ \frac{17}{7}x_2 }=\frac{p_1}{p_2}* \frac{10}{17} = 1 \\ \frac{p_1}{p_2} = \frac{17}{10}$

Затем площади:

$S_{ABC}= \frac{1}{2}(zp \: sin \alpha +yp \: sin \alpha ) = \frac{1}{2} psin \alpha (z+y) = \frac{1}{2} \times \frac{27}{17} p_1sin \alpha \times \frac{17}{7} y \\ S_{XPF}= \frac{1}{2} \times \frac{y}{2} \times p_1sin \alpha$

Следовательно, отношение площадей равно 54/7.