Найти радиус окружности, вписанной впрямоугольный треуголь
ник, периметр которого равен 32 дм, а радиус описаннои около
треутольника окружности 6 дм
Ответы
Ответ дал:
1
Ответ:
4 дм.
Объяснение:
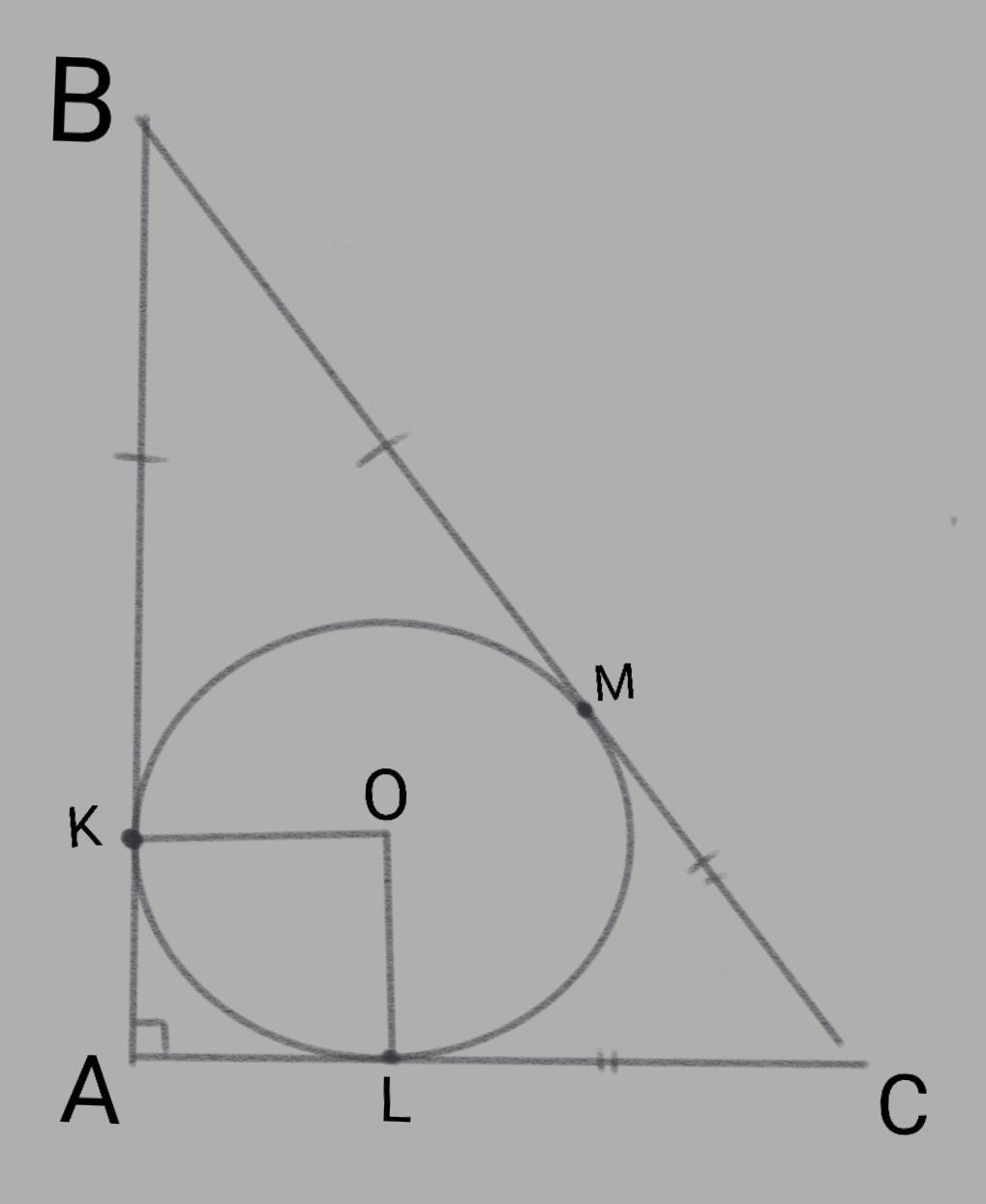
Пусть дан прямоугольный треугольник ABC с вписанной окружностью с центром O, которая касается сторон треугольника в точках K,L,M(см. рисунок)
1)Если около прямоугольного треугольника описана окружность, то гипотенуза является диаметром этой окружности, то есть BC=12дм.
2)BM=BK, LC=CM (отрезки касательных из одной точки), значит BK+LC=BM+CM=BC=12 дм.
3)Заметим, что AKOL-квадрат(OL, OK -радиусы, проведённые к точке касания + угол A=90°, OL=OK), значит AK=AL=R(радиус вписанной окружности)
4)AK+AL=P(периметр)-BC-BK-LC=32-12-12=8=2R
R=8/2=4 дм.
Приложения:
ГАЗ52:
Чертёж САМИ чертили?
Клёво.
Да, сам делал
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад