мххххххх я теряю рассудок если коротко..........
Приложения:
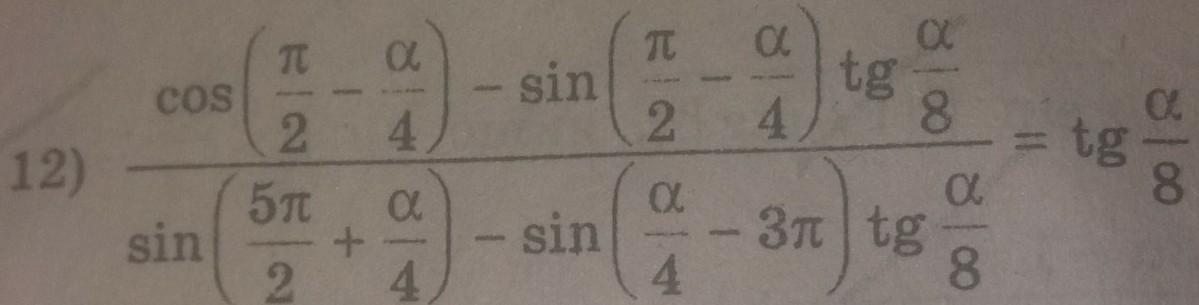
Аноним:
благо что удалили этого мозгодуба
Ответы
Ответ дал:
1
Доведення.
##################
Приложения:
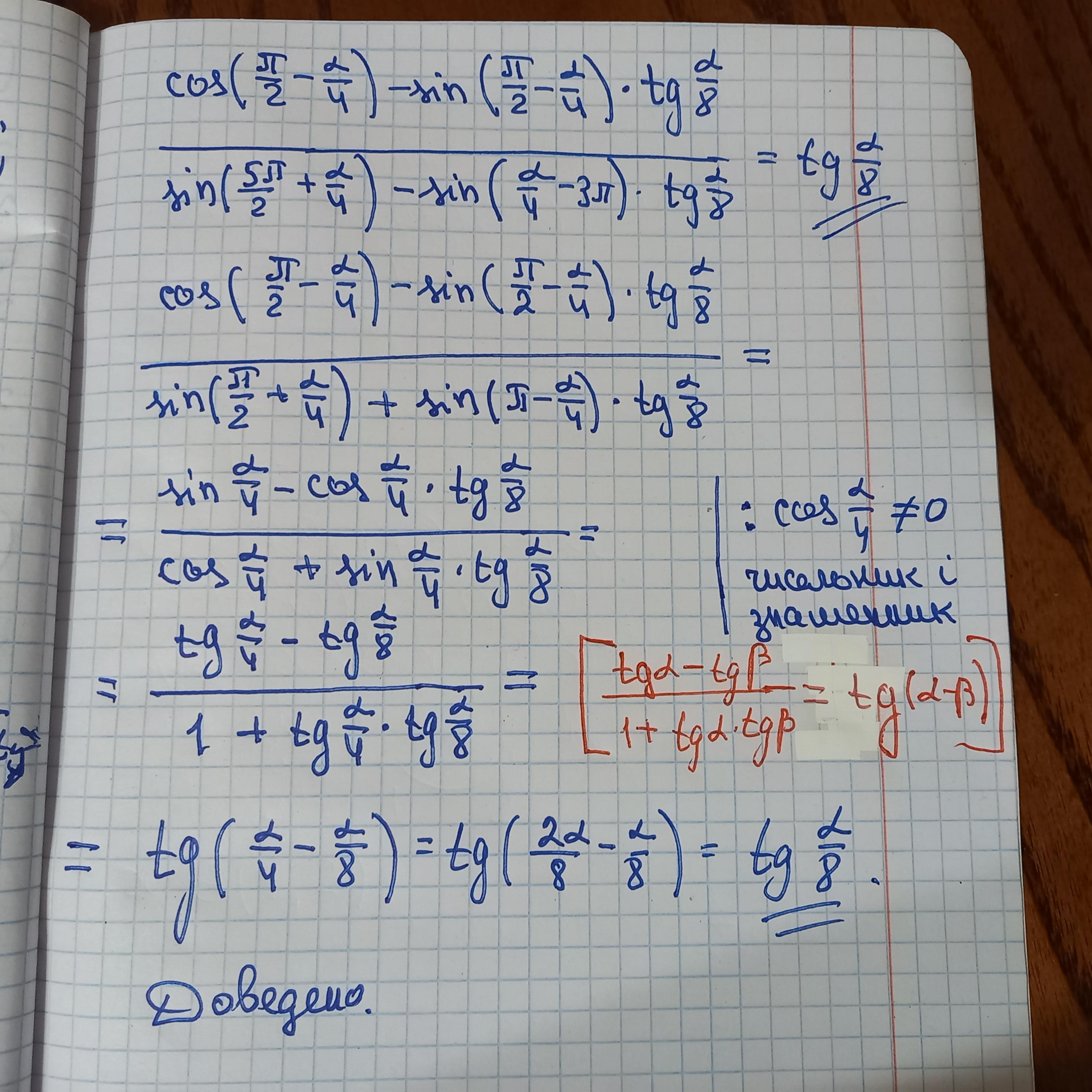
Ответ дал:
1
Ответ:
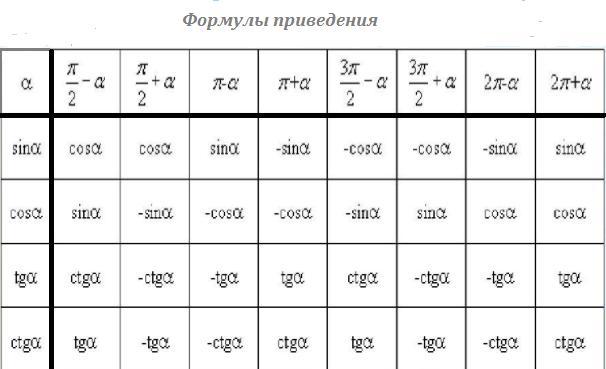
Сначала пользуемся периодичностью тригонометрических функций , применяем формулы приведения , а затем формулу тангенса разности углов .
Приложения:
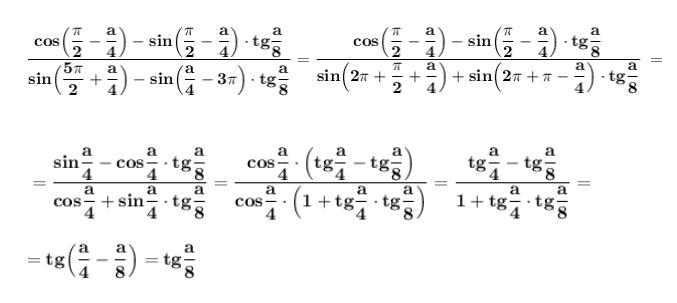
Вас заинтересует
1 год назад
1 год назад
2 года назад
8 лет назад