Ответы
Ответ дал:
1
Відповідь: zₓ' = - 3sinx - 4y .
Покрокове пояснення:
6 . z = 3cosx + 2y² - 4xy + 5 ;
zₓ' = ( 3cosx + 2y² - 4xy + 5 )ₓ' = 3 *(- sinx ) + 0 - 4 * 1 * y + 0 = -3sinx - 4y;
zₓ' = -3sinx - 4y .
Ответ дал:
1
Ответ:
Найти частные производные 1-го порядка .
Находя производную по одной из переменных, вторую считаем константой .
Приложения:
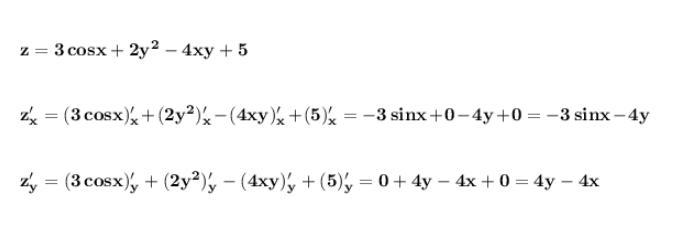
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад
