Question

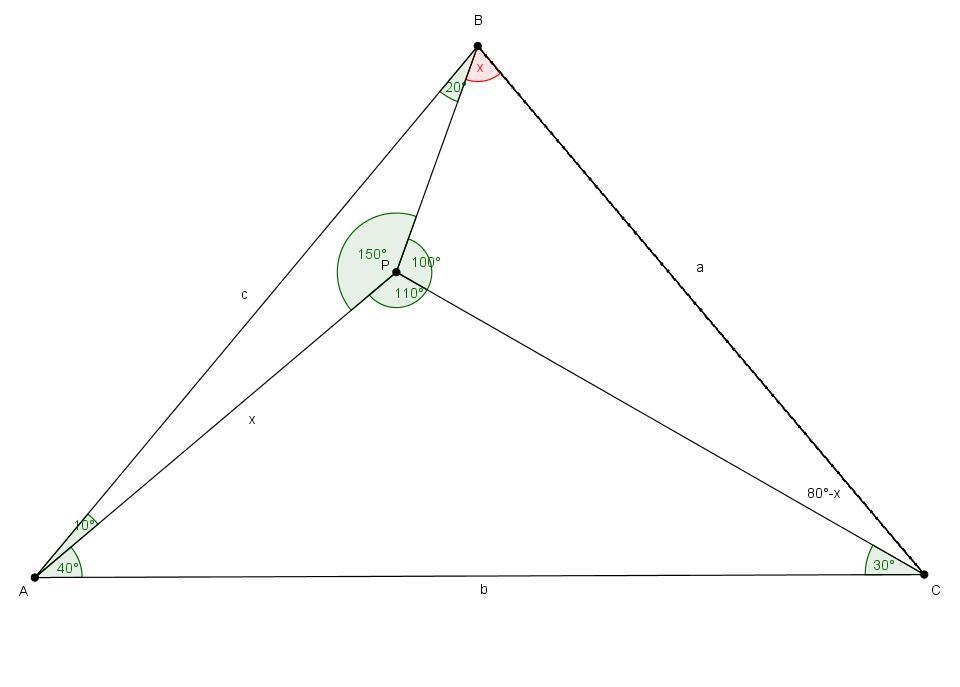
Пусть P — точка внутри треугольника ABC. Известно, что ∠BAP = 10°, ∠ABP = 20°, ∠PCA = 30° и ∠PAC = 40°. Найдите величину угла PBC

Answer 1

Ответ:

$x=60^o$

Пошаговое объяснение:

из закона синусов

1.

$\Delta ABP$

$\frac{x}{sin20^o}=\frac{c}{sin150^o}$

$\frac{x}{sin20^o}=\frac{c}{sin(90^o+60^o)}$

$\frac{x}{sin20^o}=\frac{c}{cos60^o}$

$\frac{x}{sin20^o}=\frac{c}{\frac{1}{2}}$

$\frac{x}{sin20^o}=2c\ \ \ |\cdot sin20^o$

$x=2c sin20^o$

2.

$\Delta APC$

$\frac{x}{sin30^o}=\frac{b}{sin110^o}$

$\frac{x}{\frac{1}{2}}=\frac{b}{sin(90^o+20^2)}$

$2x=\frac{b}{cos20^o}\ \ \ |:2$

$x=\frac{b}{2cos20^o}$

3.  1  и 2

$2c sin20^o=\frac{b}{2cos20^o}$

$b=4 c sin20^o cos20^o$

$b=2c \cdot 2sin20^o cos20^o$

$b=2c\cdot sin40^o$

4. из закона косинусов

$\Delta ABC$

$a^2=b^2+c^2-2bc cos50^o$

$a^2=(2c\cdot sin40^o)^2+c^2-2\cdot 2c\cdot sin40^o\cdot c\cdot cos50^o$

$a^2=4c^2sin^240^o+c^2-4c^2\cdot sin40^o cos(90^o-40^o)$

$a^2=4c^2sin^240^o+c^2-4c^2\cdot sin40^o sin40^o$

$a^2=c^2$

$\Delta ABC$ - равнобедренный

5.$\angle x$

$\angle BCA=\angle ACB$

$30^o+80^o-x=10^o+40^o$

$110^o-x=50^o$

$x=110^o-50^o$

$x=60^o$