Найдите все действительные x , удовлетворяющие неравенству (1+x+x^2)(1+x+x^2+…+x1^0)=(1+x+x^2+…+x^6)^2
antonovm:
x^10 - ? и у вас уравнение , но в любом случае сумма 3 геометрических прогрессий со знаменателем х , всё просто
точнее три суммы членов геометрических прогрессий со знаменателем х , считаете каждую и подствляете в уравнение ( неравенство )
Ответы
Ответ дал:
2
Ответ: x ∈ {-1;0}
Объяснение:
Домножим обе части на (x-1)²
При этом, подстановкой x = 1, убеждаемся что 1 не является корнем данного уравнения, поскольку правая часть уравнения полный квадрат, а левая нет
(1 + 1 +1²)(1 + 1² + ... + 1¹⁰) = 3·10 =30 ≠ k² , k ∈ N
Соответственно :
Приложения:

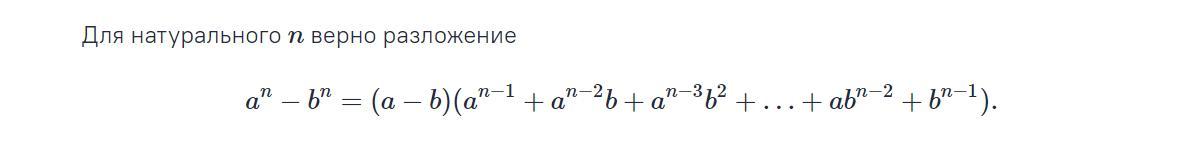
Вас заинтересует
1 год назад
1 год назад
3 года назад
3 года назад