Question

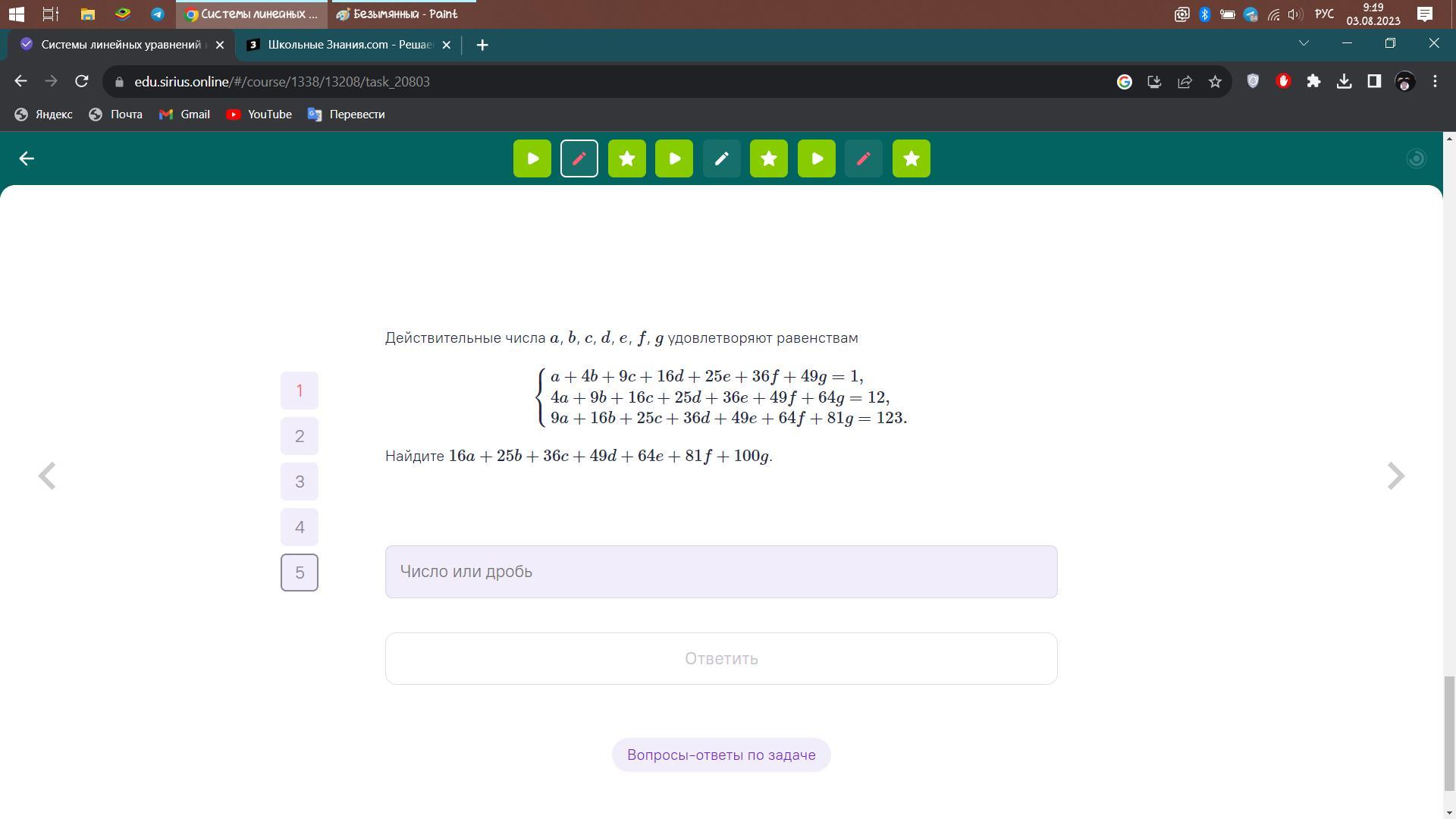
Решить задачу на скриншоте.

Answer 1

Ответ:

16·a+25·b+36·c+49·d+64·e+81·f+100·g = 334

Объяснение:

Перепишем условие в следующем виде: если

$\tt \displaystyle \left \{\begin{array}{ccc}\tt 1^2 \cdot a+2^2 \cdot b+3^2 \cdot c+4^2 \cdot d+5^2 \cdot e+6^2 \cdot f+7^2 \cdot g=1\\ \tt 2^2 \cdot a+3^2 \cdot b+4^2 \cdot c+5^2 \cdot d+6^2 \cdot e+7^2 \cdot f+8^2 \cdot g=12 \\\tt 3^2 \cdot a+4^2 \cdot b+5^2 \cdot c+6^2 \cdot d+7^2 \cdot e+8^2 \cdot f+9^2 \cdot g=123\end{array}$,

то 4²·a+5²·b+6²·c+7²·d+8²·e+9²·f+10²·g = ?

Сначала покажем, что для последовательных чисел a=n, b=n+1 и c=n+2 верно тождество: 2·b²–a²+2 = c².

В самом деле

2·(n+1)²–n²+2 = 2·n²+4·n+2–n²+2 = n²+4·n+4 = (n+2)²,

то есть 2·b²-a²+2 = c².

Применим это тождество:

3²=2·2²–1²+2

4²=2·3²–2²+2

5²=2·4²–3²+2

6²=2·5²–4²+2

7²=2·6²–5²+2

8²=2·7²–6²+2

9²=2·8²–7²+2

10²=2·9²–8²+2.

Тогда

123 = 3²·a+4²·b+5²·c+6²·d+7²·e+8²·f+9²·g =

= 2·(2²·a+3²·b+4²·c+5²·d+6²·e+7²·f+8²·g)–

–(1²·a+2²·b+3²·c+4²·d+5²·e+6²·f+7²·g)+

+2·(a+b+c+d+e+f+g) = 2·12–1+2·(a+b+c+d+e+f+g) =

= 23+2·(a+b+c+d+e+f+g).

Отсюда

2·(a+b+c+d+e+f+g) = 100 или a+b+c+d+e+f+g = 50.

Далее, вычислим нужное значение:

4²·a+5²·b+6²·c+7²·d+8²·e+9²·f+10²·g =

= 2·(3²·a+4²·b+5²·c+6²·d+7²·e+8²·f+9²·g)–

–(2²·a+3²·b+4²·c+5²·d+6²·e+7²·f+8²·g)+

+2·(a+b+c+d+e+f+g) = 2·123–12+2·(a+b+c+d+e+f+g) =

= 234+2·(a+b+c+d+e+f+g) = 234+2·50 = 334.

#SPJ1