Математика! Помогите, пожалуйста! Нужно найти площадь фигуры определяемой системой неравенств
Приложения:

aarr04594:
1/2(8×4-4×2)=1/2×24=12.
Ответы
Ответ дал:
0
Решение .
Задана область .
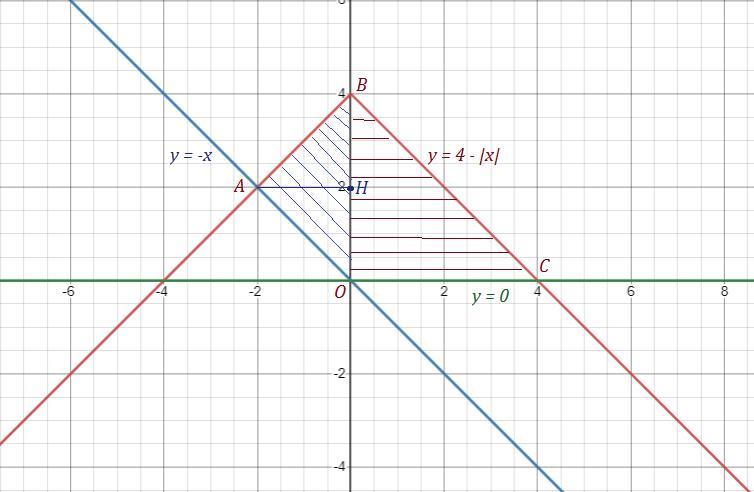
Построим графики функций: y=0 .Это ось ОХ) .
y= -x - прямая - биссектриса 2 и 4 координатные углов) .
y = 4 - |x| . Графиком является "угол" с вершиной в точке (0;4) ,
пересекает ось ОХ в точках (-4;0) и (4;0) .
Получили область , состоящую из двух треугольников: ΔАОВ и ΔВОС
В ΔАОВ основание ОВ = 4 , высота АН = 2 , площадь ΔАОВ равна
S₁ = 1/2 · 4 · 2 = 4 .
В ΔВОС оба катета равны , ОВ = ОС = 4 . Площадь ΔВОС равна
S₂ = 1/2 · 4 · 4 = 8 .
Площадь фигуры равна S = S₁ + S₂ = 4 + 8 = 12 .
Ответ: S = 12 .
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад
8 лет назад