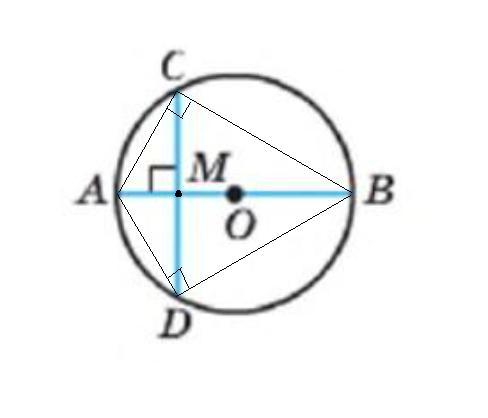
Диаметр АВ цепи с центром О перпендикулярен хорде CD. Какое из приведенных равенств неправильно?
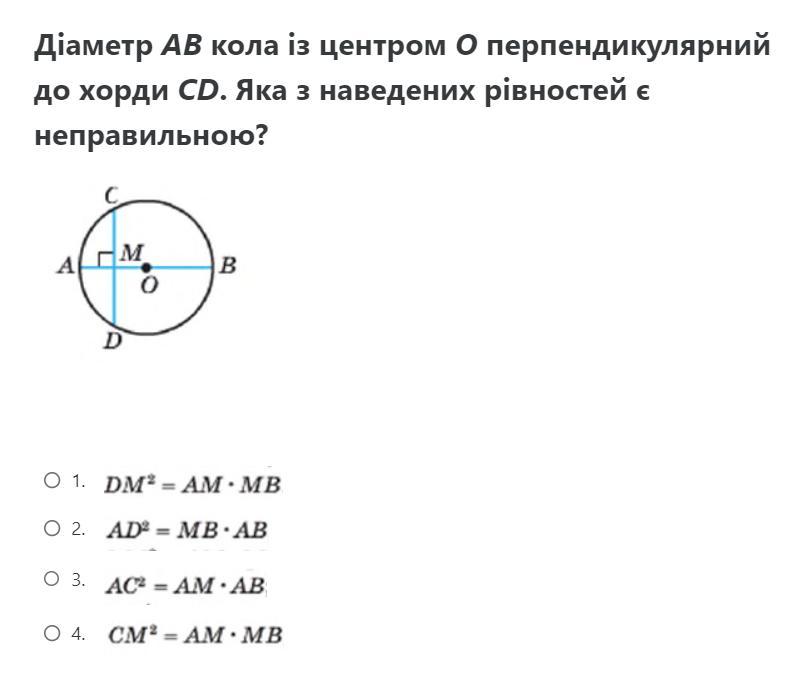
Ответы
Ответ: №2 .
Неверно равенство №2 ( АD²= МB · АВ - неверно ) .
АВ - диаметр окружности . Угол, опирающийся на диаметр - прямой .
Значит ΔАСВ и ΔАDB - прямоугольные , ∠С=90° и ∠D=90° .
Хорда CD перпендикулярна диаметру АВ . Значит СМ и DM - высоты в прямоугольных треугольниках АСВ и ADB , опущенные из прямого угла на гипотенузу .
Известны две теоремы о пропорциональных отрезках в прямоугольном треугольнике .
Теорема 1 . Высота, опущенная из вершины прямого угла на гипотенузу, есть среднее пропорциональное между проекциями катетов на гипотенузу ( между отрезками, на которые делится гипотенуза этой высотой ).
В ΔАDВ отрезок АМ - проекция катета АD на АВ , MB - проекция катета BD на АВ ⇒ DМ²= АМ · МВ , (1) - верно .
В ΔАСВ отрезок АМ - проекция катета АС на АВ , МB - проекция катета СB на АВ ⇒ СМ²= АМ · МВ , (4) - верно .
Теорема 2 . Катет прямоугольного треугольника есть среднее геометрическое между гипотенузой и проекцией этого катета на гипотенузу .
В ΔАСВ отрезок АМ - проекция катета АС на АВ ⇒ АС²= АМ · АВ , (3) - верно .
Можно было ещё получить такие верные равенства :
ВС²= ВМ · АВ , АD²= АМ · АВ , BD²= МB · АВ