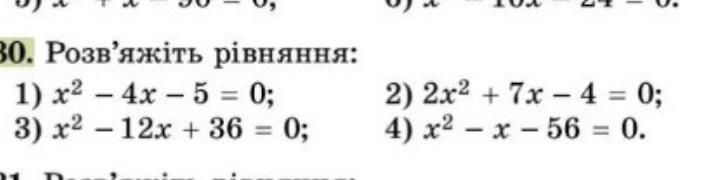Ответы
Ответ дал:
0
Ответ:
Решить квадратные уравнения .
По теореме Виета легко подобрать корни уравнения :
Левая часть уравнения представляет из себя полный квадрат :
По теореме Виета легко подобрать корни уравнения :
Решаем с помощью дискриминанта .
Приложения:


Вас заинтересует
1 год назад
1 год назад
1 год назад
2 года назад