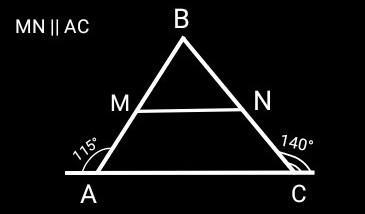
Внешние углы треугольника ABC при вершинах A и C равны 115° и 140°. Прямая, параллельная прямой AC пересекает стороны AB и AC в точках M и N.
Найдите углы треугольника BMN.
Ответы
Ответ дал:
0
Ответ:
65°, 40° и 75°
Объяснение:
∠BAC = 180° - 115° = 65°
∠BCA = 180° - 140° = 40°
∠BMN = ∠BAC и ∠BNM = ∠BCA как соответственные, т.е. ∠BMN = 65° и ∠BNM = 40°.
∠MBN = 180° - (∠BMN + ∠BNM) = 180° - (65° + 40°) = 180° - 105° = 75°.
Рисунок на фото
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад