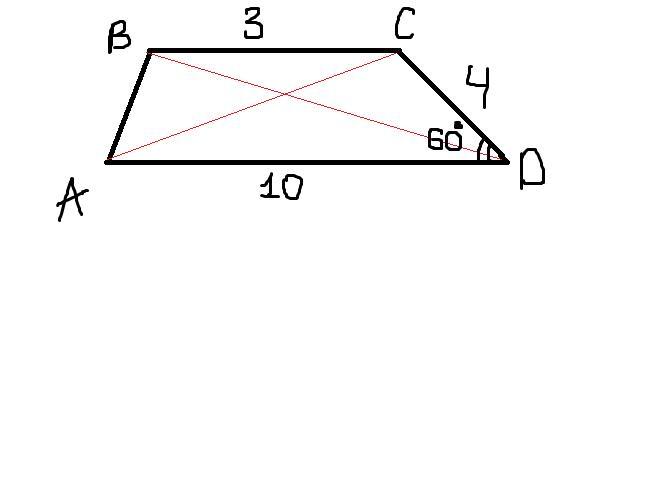
У трапеції ABCD відомо, що BC || AD, BC = 3 см, AD = 10 см,
CD = 4 см, ∠D = 60°. Знайдіть діагоналі трапеції
Ответы
Ответ дал:
2
У трикутнику ADC (див. рисунок) за Т. cos маємо:
AC^2 = CD^2 + AD^2 - 2*CD*AD*cos(D);
AC^2 = 16 + 100 - 2 * 4 * 10 * cos(60°);
AC^2 = 116 - 80 * 0,5;
AC^2 = 116 - 40;
AC^2 = 76;
AC = (см).
У трикутнику BCD (див. рисунок) маємо:
Кут C = 180° - кут D = 180° - 60° = 120°, оскільки сума кутів при бічній стороні трапеції дорівнює 180°.
У трикутнику BCD (див. рисунок) за Т. cos маємо:
BD^2 = BD^2 + CD^2 - 2*BC*CD*cos(C);
BD^2 = 9 + 16 - 2*3*4*cos(120°);
BD^2 = 25 - 24*(-0,5);
BD^2 = 25 + 12;
BD^2 = 37;
BD = (см).
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад
BD із закону косинусів для трикутника BCD