В треугольнике ABC медиана AM перпендикулярна биссектрисе BD. Найдите площадь треугольника ABC, если AM=20,BD=19.
Ответы
Ответ дал:
0
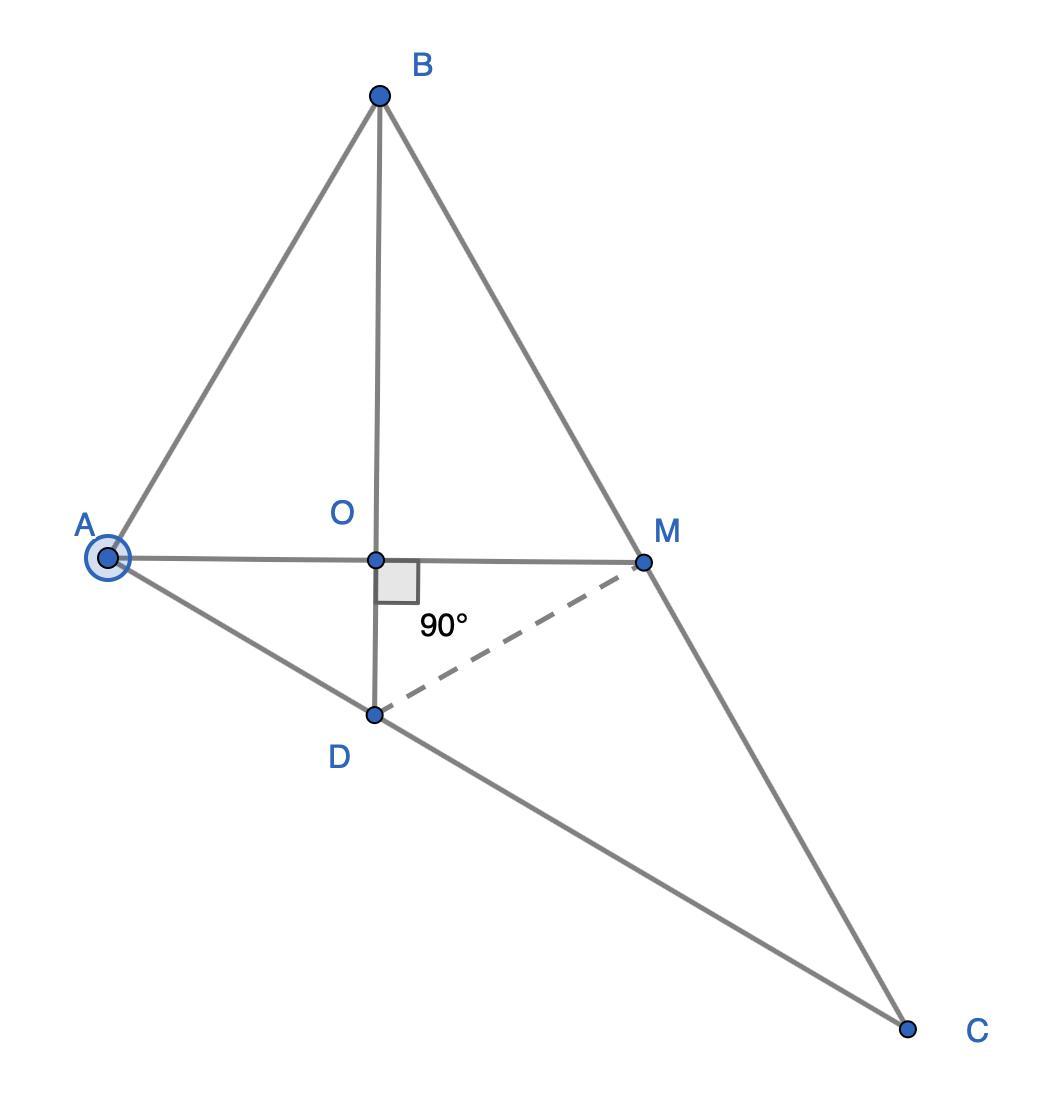
См. рисунок
Обозначим точку пересечения AM и BD как O.
Так как биссектриса BO в треугольнике ABM является по условию еще и высотой, треугольник ABM равнобедренный (AB=BM). Поэтому AO=OM = AM/2. Аналогично AD=DM, потому что DO в треугольнике ADM является и высотой и медианой.
Далее имеем
Однако а кроме того
так как медиана DM делит треугольник BDC на два равновеликих.
Окончательно получаем
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
8 лет назад