Срочно прошу!!
Два рівнобедрених трикутники мають спільну основу, а їх площини утворюють кут 60°. Спільна основа дорівнює 16 см, бічна сторона одного трикутника дорівнює 17 см, а бічні сторони другого трикутника взаємно перпендикулярні. Обчислити відстань між вер- шинами трикутника
Ответы
Відповідь: 13 cм .
Пояснення:
ΔABC i ΔABD - рівнобедрені ; АС = ВС = 17 см ; AD = BD ; AD⊥BD .
AB = 16 см ; ∠ADB = 90° .
Якщо т. М - середина основи АВ , тоді АМ = ВМ = 1/2 * АВ = 8 ( см ) .
СМ⊥АВ , DM⊥AB , то ∠CMD = 60° .
Із прямок. ΔАМС МС = √( АС² - АМ² ) = √( 17² - 8² ) = 15 ( см ) ;
Із ΔCMD за Т. косинусів CD = √( MC²+ MD²- 2MC*MD*cos∠CMD ) =
= √( 15² + 8² - 2*15*8* cos60°) = √( 225 + 64 -60 * 1/2 ) =√169 = 13 (см ).
CD = 13 cм .
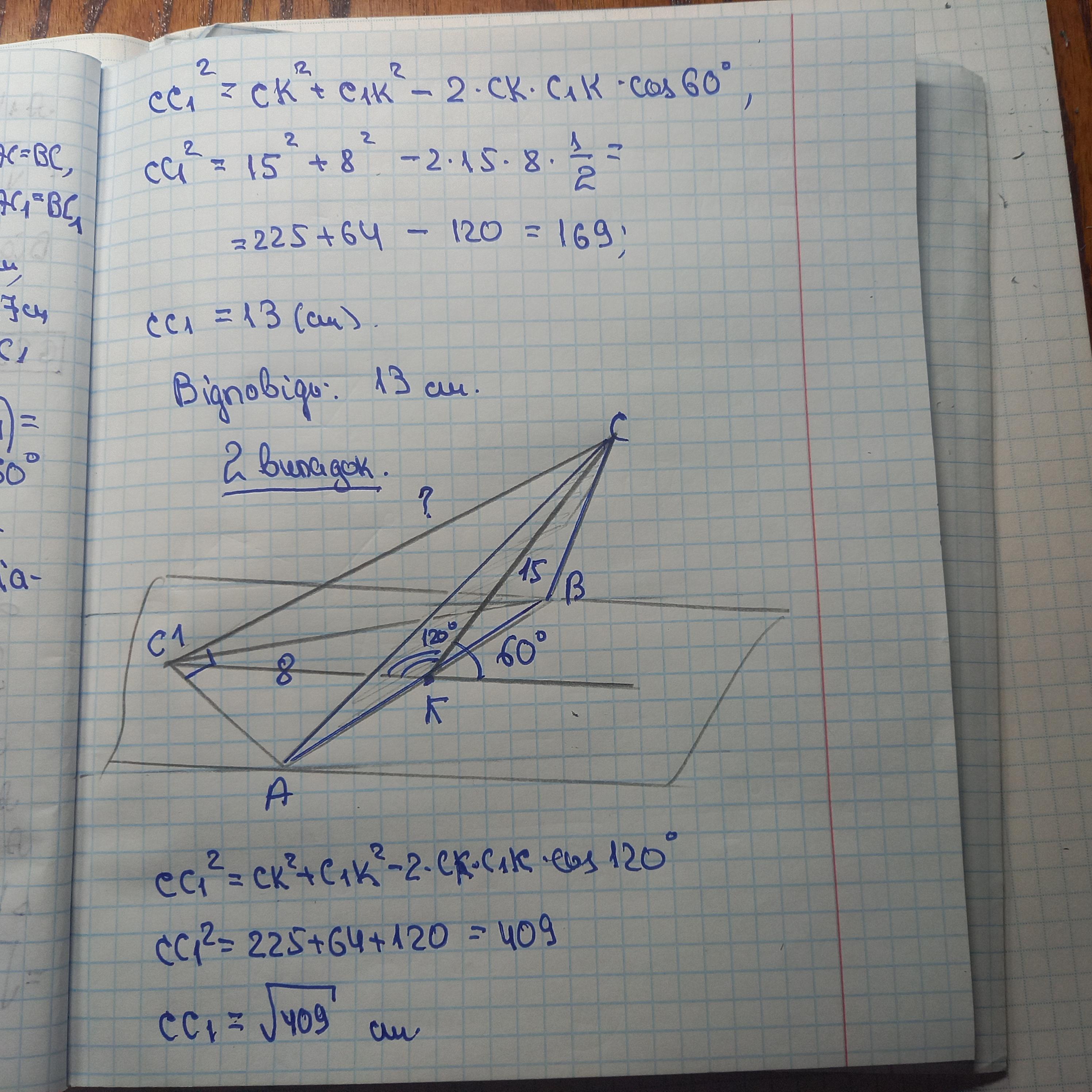
Відповідь: 13 см або √409 см.
Пояснення:
Зазвичай в таких задачах забувають, що дано кут між площинами, яким належать трикутники. Кут між площинами 60°, але це не означає, що кут між трикутниками тільки 60°. Кут між трикутниками може бути і 120°. Тому відстань між вершинами набуває двох значень в залежності від розташування трикутників. Іноді в умові дають підказку, коли пишуть "скільки розв'язків має задача " або "розгляньте два випадки".