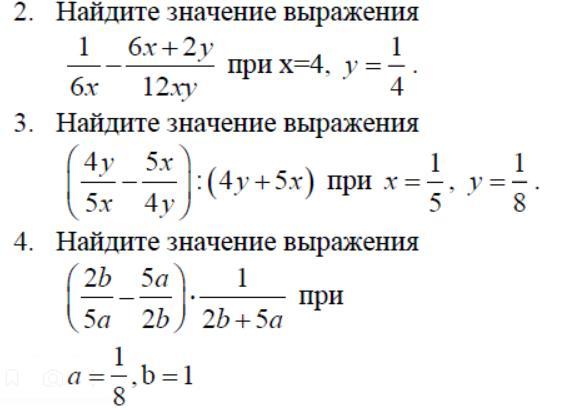Question

Алгебра 100 баллов, с решением пожалуйста

Answer 1

Ответ:

Значения выражений:

2.   -2;   3.   -1;   4.   1,1

Объяснение:

2.   Найти значение выражения:

$\displaystyle \bf \frac{1}{6x}-\frac{6x+2y}{12xy}$     при     х = 4, у = 1/4

Сначала упростим выражение.

Приведем дроби к общему знаменателю.

$\displaystyle \frac{1}{6x}^{(2y}-\frac{6x+2y}{12xy}^{(1}=\frac{2y-6x-2y}{12xy} =-\frac{6x}{12xy}=-\frac{1}{2y}$

y = 1/4

$\displaystyle \bf - \frac{1}{2\cdot\frac{1}{4} }=-\frac{1}{\frac{1}{2} }=-2$

3.   Найти значение выражения:

$\displaystyle \bf \left(\frac{4y}{5x}-\frac{5x}{4y} \right):(4y+5x)$     при   х = 1/5; у = 1/8

Приведем дроби в скобках к общему знаменателю.

$\displaystyle \left(\frac{4y}{5x}^{(4y}-\frac{5x}{4y} ^{(5x} \right):(4y+5x)=\frac{16y^2-25x^2}{20xy} \cdot \frac{1}{4y+5x}=$

• Разность квадратов двух чисел:

       a² - b² = (a - b)(a + b)

$\displaystyle \frac{(4y-5x)(4y+5x)}{20xy\cdot(4y+5x)} =\frac{4y-5x}{20xy}$

х = 1/5; у = 1/8

$\displaystyle \frac{4\cdot\frac{1}{8}-5\cdot\frac{1}{5} }{20\cdot\frac{1}{5}\cdot\frac{1}{8} } =\frac{\frac{1}{2} -1}{\frac{1}{2} } =-\frac{1}{2}:\frac{1}{2}=\bf -1$

4.   Найти значение выражения:

$\displaystyle \bf \left(\frac{2b}{5a}-\frac{5a}{2b}\right)\cdot\frac{1}{2b+5a}$     при     a = 1/8; b = 1

Приведем дроби в скобках к общему знаменателю.

$\displaystyle \left(\frac{2b}{5a}^{(2b}-\frac{5a}{2b}^{(5a}\right)\cdot\frac{1}{2b+5a}=\frac{4b^2-25a^2}{10ab} \cdot\frac{1}{2b+5a} =\\=\frac{(2b-5a)(2b+5a)}{10ab(2b+5a)} =\frac{2b-5a}{10ab}$

a = 1/8; b = 1

$\displaystyle \frac{2\cdot1-5\cdot\frac{1}{8} }{10\cdot\frac{1}{8}\cdot1 } =\frac{11}{8}:\frac{5}{4}=\frac{11\cdot4}{8\cdot5} =\frac{11}{10}=\bf 1\frac{1}{10}=1,1$

#SPJ1