Ответы
Ответ дал:
1
Ответ:
Доказано, что четырехугольник ABCD является ромбом, но не квадратом.
Объяснение:
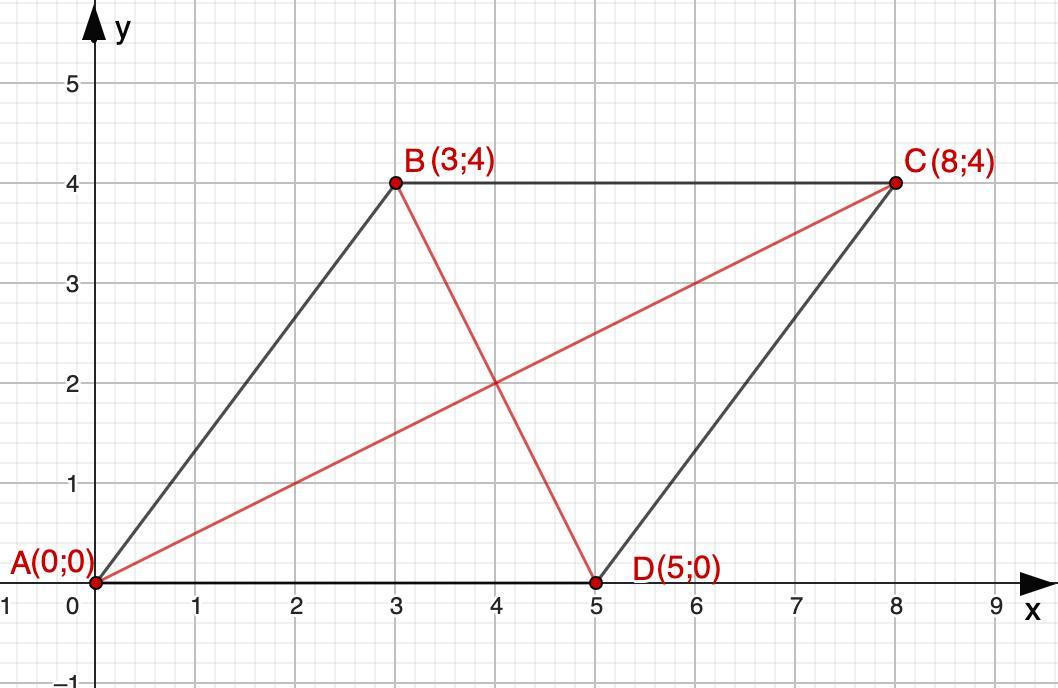
Докажите что четырехугольник ABCD с вершинами A(0;0), B(3;4), С(8;4), D(5;0) - ромб , но не квадрат.
Четырехугольник, у которого все стороны равны, либо ромб, либо квадрат.
Отличия в длине диагоналей. У квадрата они равны, а у ромба - нет.
Найдем длины сторон четырехугольника.
- Если даны две точки А(х₁; у₁) и В(х₂; у₂), то длина отрезка равна:
1) A(0;0), B(3;4)
2) B(3;4), C(8;4)
3) C(8;4), D(5;0)
4) A(0;0), D(5;0)
Стороны равны.
Сравним длину диагоналей.
1) A(0;0), С(8;4)
1) B(3;4), D(5;0)
⇒ четырехугольник ABCD является ромбом, но не квадратом.
#SPJ1
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад
8 лет назад