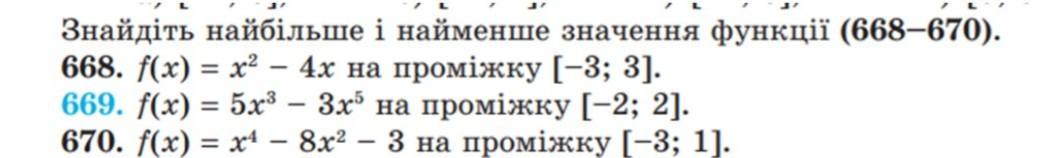Ответы
Ответ:
N670
f(x)= x⁴–8x²–3, [–3; 1].
Производная:
f '(x)= 4x³–16x=4x(x²–4)=4x(x–2)(x+2).
Точки х=–2, x=0 и x=2 являются критическими.
Точка х=2 не принадлежит заданному промежутку [–3; 1].
Вычислим значения функции в подходящих точках (х=–3, х=–2, х=0 и х=1):
f(–3)= (–3)⁴–8•(–3)²–3=81–72–3= 6.
f(–2)= (–2)⁴–8•(–2)²–3=16–32–3 = –16–3= –19.
f(0)= 0⁴–8•0²–3= 0–3= –3.
f(1)= 1⁴–8•1²–3= 1–8–3= –10.
Среди данных значений находим наибольшее и наименьшее и получаем ответ.
min f(x) = f(–2)= –19.
[–3; 1]
max f(x)= f(–3)= 6.
[–3; 1].
N669
Функция f(x) = x² - 4x на промежутке [-3; 3]:
Для начала, посчитаем значения функции при x = -3, -2, -1, 0, 1, 2 и 3:
Подставим x = -3: f(-3) = (-3)² - 4(-3) = 9 + 12 = 21
Подставим x = -2: f(-2) = (-2)² - 4(-2) = 4 + 8 = 12
Подставим x = -1: f(-1) = (-1)² - 4(-1) = 1 + 4 = 5
Подставим x = 0: f(0) = 0² - 4(0) = 0
Подставим x = 1: f(1) = 1² - 4(1) = 1 - 4 = -3
Подставим x = 2: f(2) = 2² - 4(2) = 4 - 8 = -4
Подставим x = 3: f(3) = 3² - 4(3) = 9 - 12 = -3
Таким образом, значения функции f(x) на промежутке [-3; 3] равны:
f(-3) = 21, f(-2) = 12, f(-1) = 5, f(0) = 0, f(1) = -3, f(2) = -4, f(3) = -3.
N668
Функция f(x) = 5x³ - 3x⁵ на промежутке [-2; 2]:
Аналогично, посчитаем значения функции при x = -2, -1, 0, 1 и 2:
Подставим x = -2: f(-2) = 5(-2)³ - 3(-2)⁵ = -40 - 48 = -88
Подставим x = -1: f(-1) = 5(-1)³ - 3(-1)⁵ = -5 + 3 = -2
Подставим x = 0: f(0) = 5(0)³ - 3(0)⁵ = 0
Подставим x = 1: f(1) = 5(1)³ - 3(1)⁵ = 5 - 3 = 2
Подставим x = 2: f(2) = 5(2)³ - 3(2)⁵ = 40 - 48 = -8
Таким образом, значения функции f(x) на промежутке [-2; 2] равны:
f(-2) = -88, f(-1) = -2, f(0) = 0, f(1) = 2, f(2) = -8.