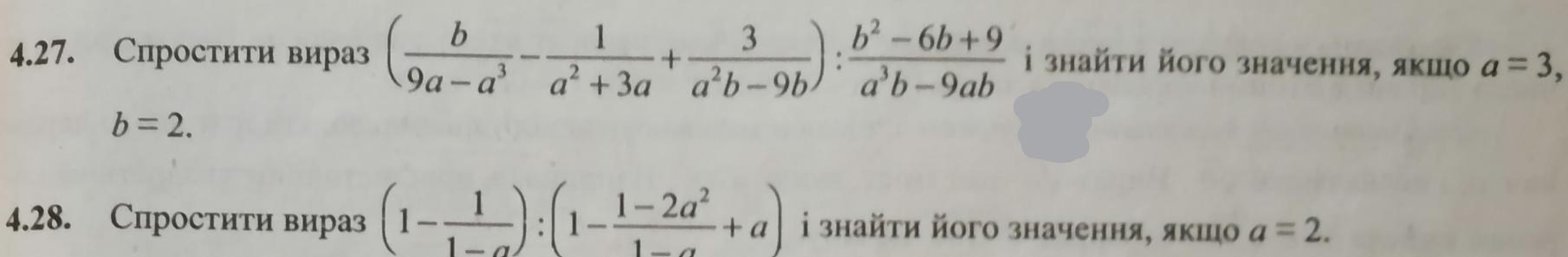Ответы
Ответ дал:
1
Ответ:
Значение выражения, если а = 3; b = 2, равно 5.
Объяснение:
4.27 Упростить выражение:
и найти его значение, если а = 3; b = 2.
Упростим сначала выражение в скобках.
В знаменателях вынесем общий множителей. Приведем дроби к общему знаменателю и выполним сложение.
- Разность квадратов двух чисел:
a² - b² = (a - b)(a + b)
В знаменателе первой дроби вынесем (-1)
Числитель разложим на множители способом группировки:
- Квадрат разности двух чисел:
(a - b)² = a² - 2ab + b²
Теперь выполним деление:
Найдем значение выражения, если а = 3, b = 2.
#SPJ1
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
8 лет назад