Question

ДАМ 40 БАЛІВ!!!! ТЕРМІНОВО!!!!!.Точка дотику кола, вписаного в прямокутну трапецію, ділить її більшу основу на відрізки 20 і 25 см. Обчисліть периметр трапеції. Я вже почала зараз прикріплю фото, продовжіть цим же методом, якщо можна!!

Answer 1

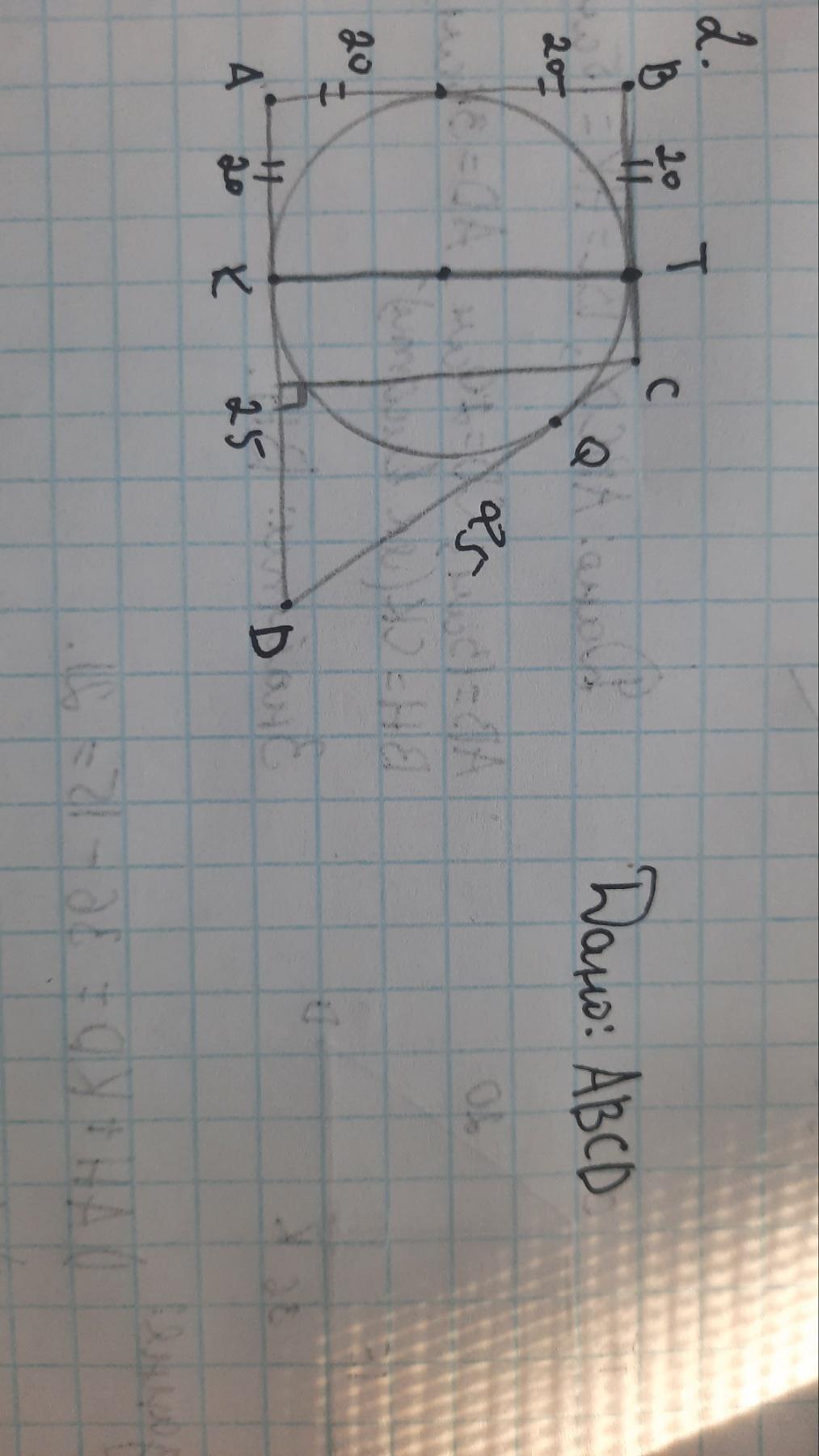
Отрезки касательных из одной точки равны. Отсюда свойство и признак описанного четырехугольника: суммы его противоположных сторон равны, P=2(AB+CD).

Видим, что из четырех пар отрезков неизвестны только CT=CQ.

Проведем биссектрисы OC и OD (центр вписанной окружности - пересечение биссектрис). Биссектрисы внутренних углов при параллельных перпендикулярны, COD=90. OQ - высота из прямого угла, OQ^2=CQ*QD.

Радиус OQ=AK=20

20^2=CQ*25 => CQ=16

CD=16+25=41

P=2(40+41)=162