Question

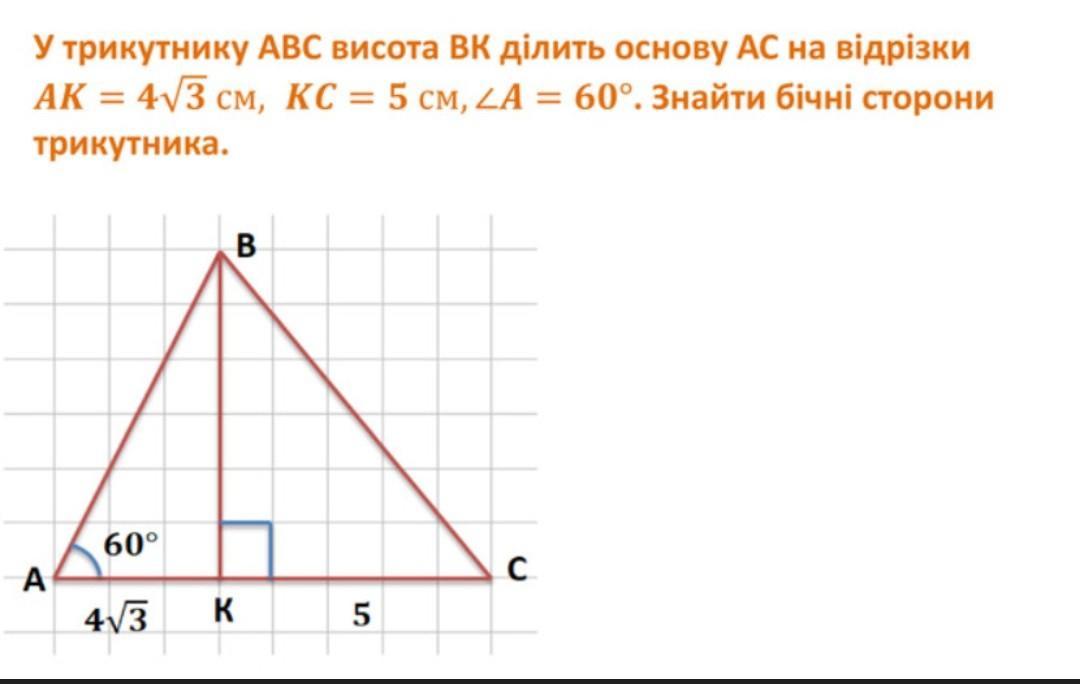
У трикутнику ABC висота ВК ділить основу АС на відрізки АК = 4√3 см, КС = 5 см,
очень срочно!!​

Answer 1

Ответ:

АВ = 8√3 см; ВС = 13 см

Объяснение:

1. В прямоугольном ∆АВК;

а) < АВК = 90° - < А = 90° - 60° = 30°;

б) катет АК лежит против угла 30°;

следовательно равен половине гепотинузы АВ, из чего следует, что:

АВ = 2 • АК = 2 • 4√3 = 8√3 см;

с) катет ВК равен произведению гепотинузы АВ на минус угла <А:

ВК = АВ• sin<60° = 8√3 • √3/2 = 8 • 3 : 2 = 12 см.

2. В прямоугольном треугольнике ВКС гепотинуза ВС, ровна:

ВС = √(КС2 + ВК2) = √(5 (в квадрате) + 12 (в квадрате)) = √(25 + 144) = √169 = 13 см

Ответ: АВ = 8√3 см; ВС = 13 см