Question

Помогите решить задачу по геометрии Пж
задание на скрине

Answer 1

Ответ:

АВ равен 12√2 см.

Объяснение:

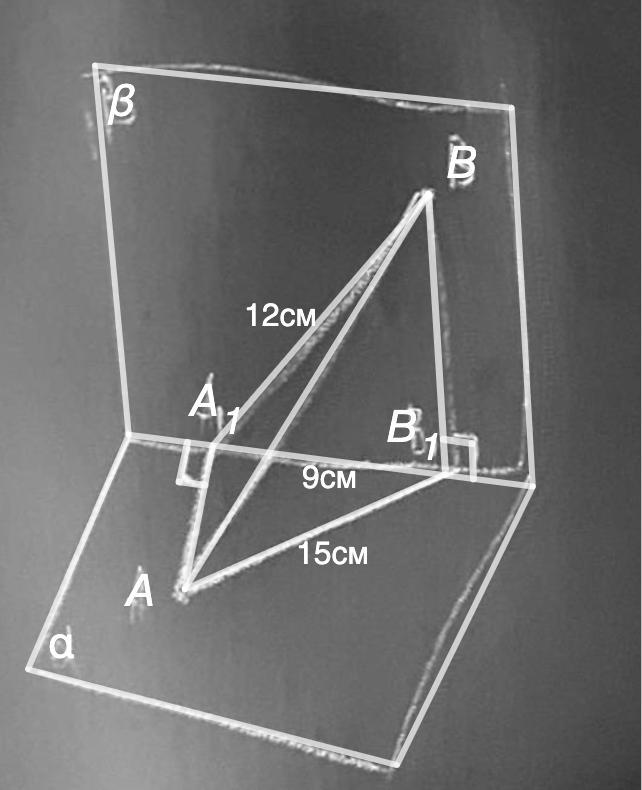
Дано: α ⊥ β;

А ∈ α; В ∈ β;

АА₁ ⊥ А₁В₁; ВВ₁ ⊥ А₁В₁;

А₁В = 12 см; АВ₁ = 15 см; А₁В₁ = 9 см.

Найти: АВ.

Решение:

α ⊥ β; АА₁ ⊥ А₁В₁; ВВ₁ ⊥ А₁В₁.

• Если прямая принадлежит одной из двух взаимно перпендикулярных плоскостей и перпендикулярна линии их пересечения, то эта прямая перпендикулярна другой плоскости.

⇒ АА₁ ⊥ β; ВВ₁ ⊥ α

Рассмотрим ΔА₁ВВ₁ - прямоугольный.

А₁В = 12 см; А₁В₁ = 9 см

• Теорема Пифагора:
• Квадрат гипотенузы равен сумме квадратов катетов.

⇒ А₁В² = А₁В₁² + ВВ₁²

144 = 81 + ВВ₁²   ⇒   ВВ₁² = 144 - 81 = 63

Рассмотрим ΔАВВ₁.

• Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой, лежащей в этой плоскости.

⇒ ВВ₁ ⊥ АВ₁   ⇒   ΔАВВ₁ - прямоугольный.

По теореме Пифагора:

АВ² = ВВ₁² + АВ₁²

АВ² = 63 + 225 = 288   ⇒   АВ = √288 = 12√2 (см)

АВ равен 12√2 см.

#SPJ1