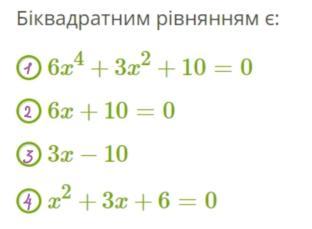Question

Помогите пожалуйста!

Answer 1

Пояснення:

1)

$x^4+x^2-20=0$

Нехай х²=u≥0        ⇒

$u^2+u-20=0\\\\u^2+5u-4u-20=0\\\\u*(u+5)-4*(u+5)=0\\\\(u+5)*(u-4)=0\\\\u+5=0\\\\u=x^2=-5\ \notin\ (x^2\geq 0).\\\\u-4=0\\\\u=x^2=4\\\\x_1=-2\ \ \ \ x_2=2.$

Відповідь: х₁=-2,   х₂=2.

2)

$x^4-4x^2+12=0$

Нехай х²=u≥0        ⇒

$u^2-4u+12=0\\\\D=(-4)^2-4*1*12=16-48=-32. \ \ \ \ \ \ \Rightarrow$

Оскільки дискриминант меньший за нуль, то рівняння не має дійсних рішень.

3)

$x*(x-1)*(x-2)*(x-3)=24\\\\(x*(x-3))*((x-1)*(x-2))=24\\\\(x^2-3x)*(x^2-x-2x+2)=24\\\\(x^2-3x)*(x^2-3x+2)=24$

Нехай х²-3x=t      ⇒

$t*(t+2)=24\\\\t^2+2t-24=0\\\\t^2+6t-4t-24=0\\\\t*(t+6)-4*(t+6)=0\\\\(t+6)*(t-4)=0\\\\t+6=0\\\\x^2-3x+6=0\\\\D=(-3)^3-4*1*6=9-24=-15 \notin\\\\t-4=0\\\\x^2-3x-4=0\\\\x^2-4x+x-4=0\\\\x*(x-4)+(x-4)=0\\\\(x-4)*(x+1)=0\\\\x-4=0\\\\x_1=4.\\\\x+1=0\\\\x_2=-1.$

Відповідь: х₁=4,    х₂=-1.

4)

Відповідь: біквадратним рівнянням є 6х⁴+3х²+10=0.