Математический Анализ! ДАЮ 100 баллов
ПРИМЕР (Г)
Доказать равенство используя метод математической индукции
Не могу понять как дальше работать с n-1
Прошу полностью расписать ответ.
Приложения:
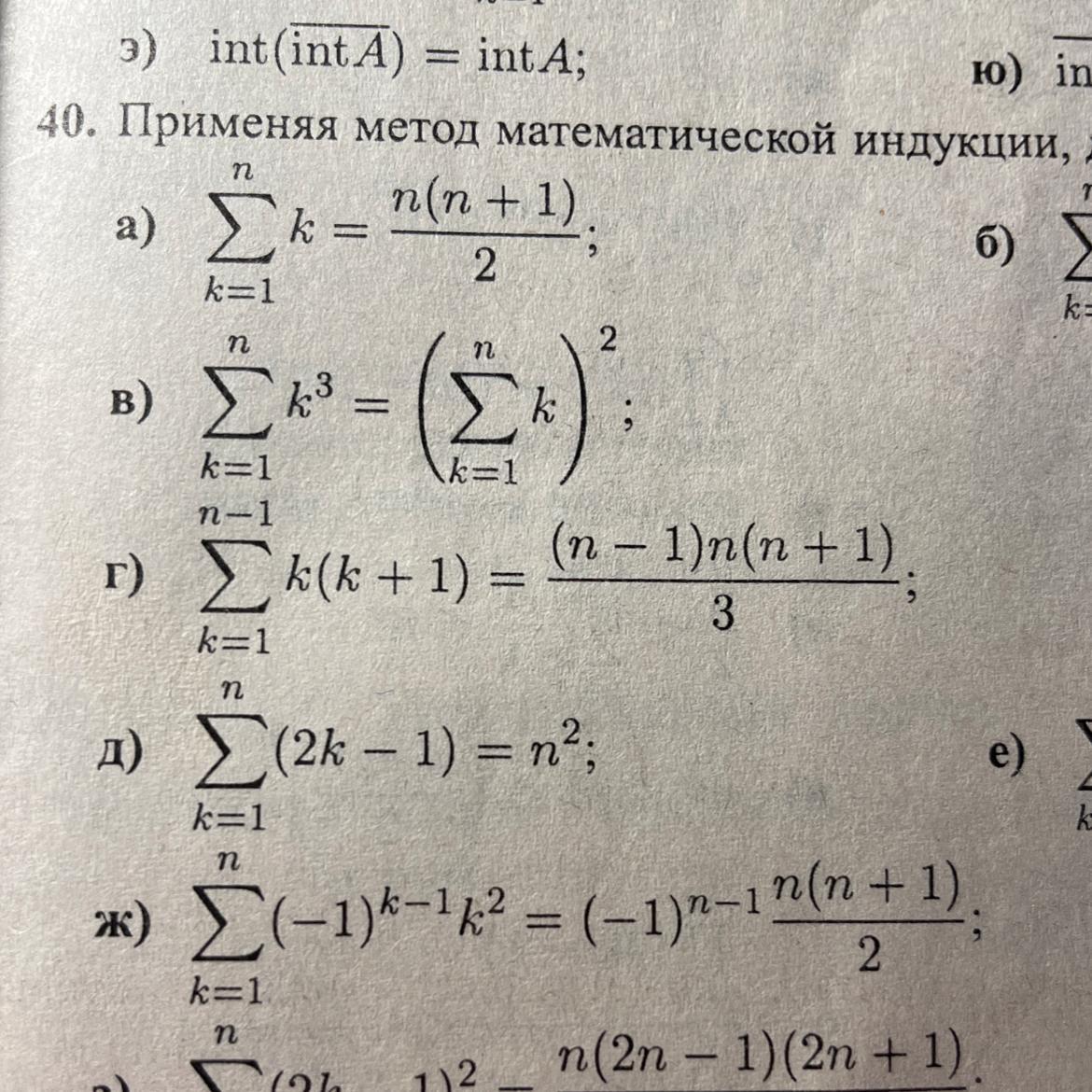
Ответы
Ответ дал:
1
База индукции: При , левая часть равенства равна 0, так как сумма пуста. Правая часть равенства также равна 0. Таким образом, утверждение верно для
.
Шаг индукции: Предположим, что утверждение верно для некоторого , то есть:
Теперь докажем, что утверждение верно и для . Для этого добавим к обеим частям равенства слагаемое
:
Правую часть можно привести к общему знаменателю и упростить:
Таким образом, если утверждение верно для n=k, то оно верно и для .
Исходя из принципа математической индукции, утверждение верно для всех натуральных чисел n.
******************************************************************************************
Если вам трудно воспринимать индукционный переход, то можно сделать упрощение следующим образом
При имеем:
plus3809725276:
Можете обновить страницу. Добавил третий пункт упрощенный вид
вижу, спасибо большое
Вас заинтересует
1 год назад
1 год назад
1 год назад
2 года назад
8 лет назад