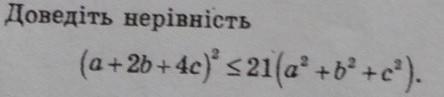Question

помогите срочно алгебра​

Answer 1

Відповідь:

Спочатку розкриємо квадрат на лівій стороні:
(a+2b+4c)2=a2+4ab+16ac+4b2+16bc+16c2

Тепер можемо виразити праву частину нерівності:
21(a2+b2+c2)=21a2+21b2+21c2
Тепер давайте порівняємо отримані вирази:

a2+4ab+16ac+4b2+16bc+16c2≤21a2+21b2+21с2
Тепер віднімемо від обох сторін нерівності вираз:
a2+4ab+16ac+4b2+16bc+16c2:0≤20a2+20b2+20c2−4ab−16ac−16bc

Тепер можемо поділити обидві сторони на 4 (так як коефіцієнт 4 більше нуля і може бути виокремлений):

0≤5a2+5b2+5c2−ab−4ac−4bc
Таким чином, ми довели нерівність:
(a+2b+4c)2≤21(a2+b2+c2)

або

0≤5a2+5b2+5c2−ab−4ac−4bc

Пояснення: