Срочно зробіть знайти матрицю F(A)
Приложения:
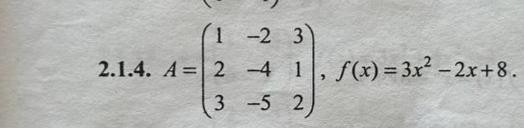
fuzey5721:
Братан ти випадково не в НАУ вчишся?
Нє,а шо?
та єбат просто у мене такі самі завдання
Ответы
Ответ дал:
1
Ответ:
Пошаговое объяснение:
Для того, щоб знайти матрицю , де
- це дана матриця, а
- це дана функція, нам потрібно застосувати функцію
до кожного елемента матриці
.
Тобто, якщо
,
то
В даному випадку, , тому ми отримаємо:
.
Тепер ми можемо обчислити значення для кожного
:
,
,
,
,
,
.
Отже,
Брат мені хелпани ти рал круто пишеш
Try \cdot instead of *
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
8 лет назад