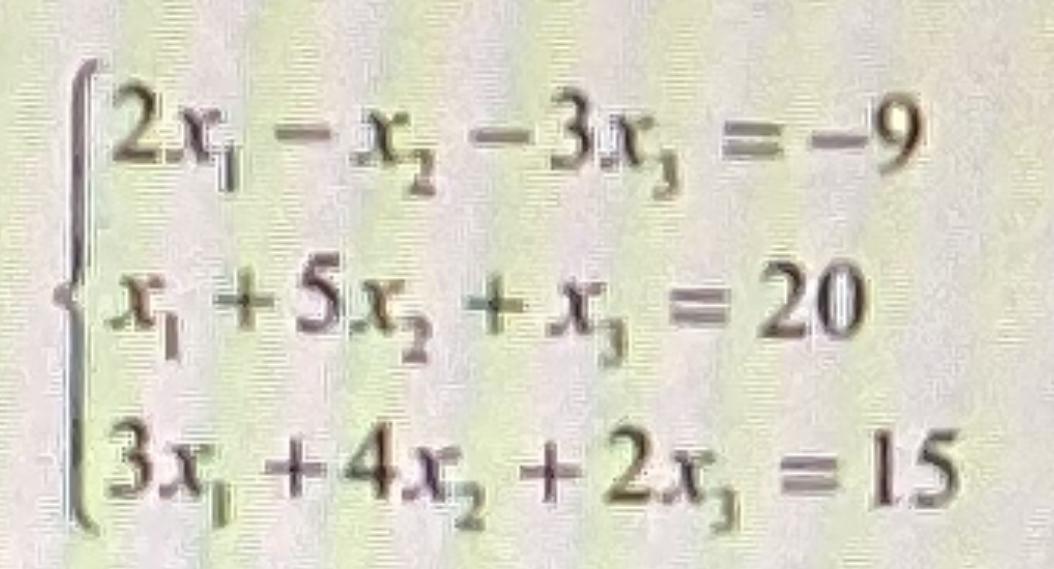Ответы
Ответ дал:
1
Це система лінійних рівнянь. вирішити її можна за допомогою методу методу виключення.
1. Помножимо друге рівняння на 2 і віднімемо його від першого рівняння:
Це дасть нове рівняння:
2. Помножимо друге рівняння на 3 і віднімемо його від третього рівняння:
Це дасть друге нове рівняння:
3. Тепер у нас є система двох рівнянь з двома невідомими
Додамо ці два рівняння:
Отже,
4. Підставимо назад у перше і друге рівняння, щоб знайти
і
:
Розв'язавши ці два рівняння, отримаємо:
,
Отже, розв'язок системи рівнянь є:
,
,
Вас заинтересует
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад