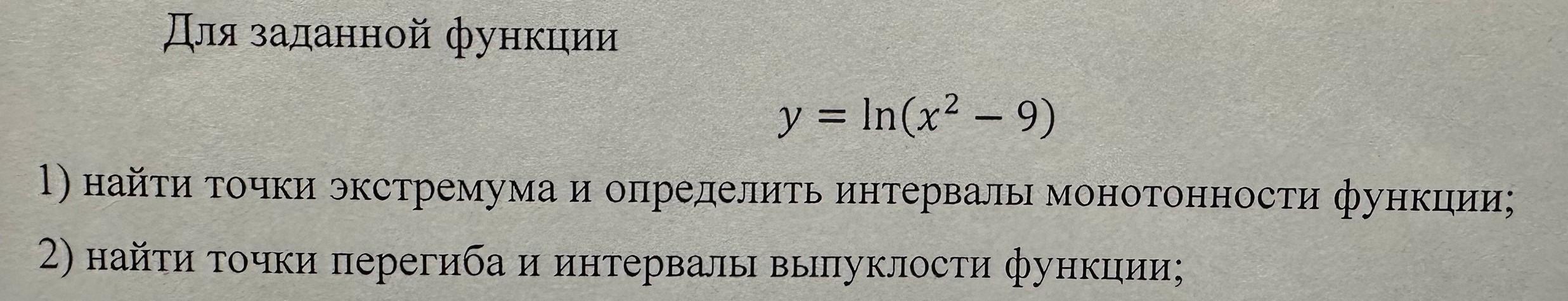Question

Помогите, пожалуйста, с полным решением

Answer 1

Ответ:

Чтобы решить эту задачу, нам потребуется взять производные функции y = ln(x² - 9) и проанализировать их.

1) Чтобы найти точки экстремума и интервалы монотонности функции, найдем первую и вторую производные функции y = ln(x² - 9).

Первая производная:

dy/dx = 1/(x² - 9) * 2x

Вторая производная:

d²y/dx² = (2/(x² - 9) - 4x²)/(x² - 9)²

Теперь мы можем найти значения x, приравнивая производные к нулю и анализировать знаки производных в разных интервалах.

Для первой производной:

dy/dx = 1/(x² - 9) * 2x = 0

Решив эту уравнение, получим две критические точки x = -3 и x = 3.

Подставляя значения x = -3 и x = 3 обратно в функцию, находим соответствующие значения y:

При x = -3: y = ln((-3)² - 9) = ln(0) - не определено

При x = 3: y = ln((3)² - 9) = ln(0) - не определено

Таким образом, у нас присутствуют точки разрыва на оси x при x = -3 и x = 3.

Теперь мы должны анализировать знаки первой производной на разных интервалах:

- При x < -3 первая производная отрицательна.

- При -3 < x < 3 первая производная положительна.

- При x > 3 первая производная отрицательна.

Итак, интервалы монотонности функции выглядят следующим образом:

- Функция монотонно убывает на интервале (-∞, -3).

- Функция монотонно возрастает на интервале (-3, 3).

- Функция монотонно убывает на интервале (3, +∞).

2) Чтобы найти точки перегиба и интервалы выпуклости функции, проанализируем знак второй производной.

Для второй производной:

d²y/dx² = (2/(x² - 9) - 4x²)/(x² - 9)² = 0

Здесь нет решений, поэтому нет точек перегиба.

Чтобы найти интервалы выпуклости, проанализируем знаки второй производной на разных интервалах:

- На интервале (-∞, -3) вторая производная положительна.

- На интервале (-3, 3) вторая производная отрицательна.

- На интервале (3, +∞) вторая производная положительна.

Таким образом, интервалы выпуклости функции следующие:

- Функция выпуклая вниз на интервале (-∞, -3).

- Функция вогнута вверх на интервале (-3, 3).

- Функция выпуклая вниз на интервале (3, +∞).

Answer 2

Ответ:

1) функция убывает на промежутке  (-∞; -3);

возрастает на промежутке  (3; +∞).

Точек экстремумов нет.

2) функция выпукла на промежутках (-∞; -3), (3; +∞).

Точек перегиба нет.

Объяснение:

Дана функция: у = ln(x² - 9)

1) найти точки экстремума и определить интервалы монотонности функции;

2) найти точки перегиба и интервалы выпуклости функции;

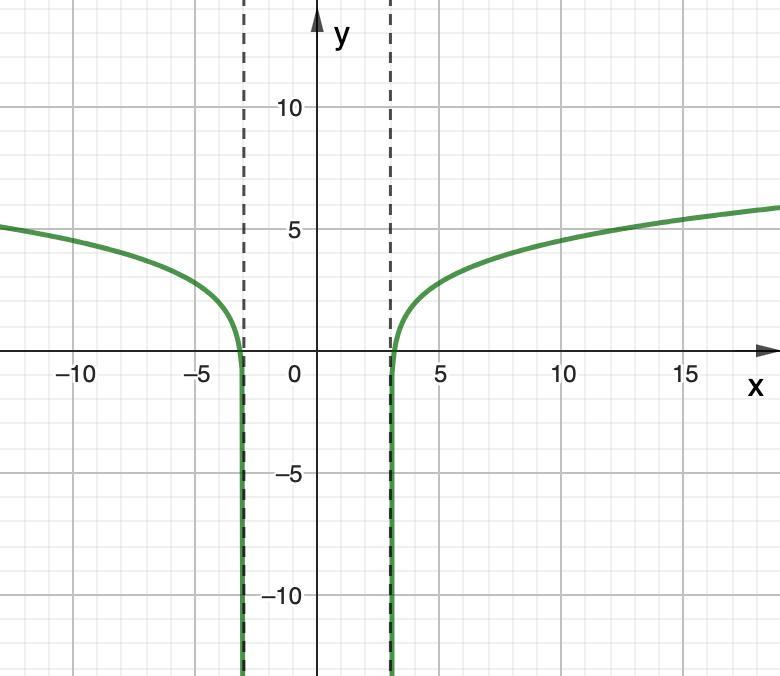
Для начала найдем область определения данной функции:

х² - 9 > 0

(x - 3)(x + 3) > 0

$+++(-3)---(3)+++$

⇒ D(y) = (-∞; -3) ∪ (3; +∞)

То есть, график данной функции расположен левее х = -3 и правее х = 3.

1) Найдем производную, приравняем к нулю и найдем корни.

$\displaystyle y'=\frac{(x^2-9)'}{x^2-9} =\frac{2x}{(x-3)(x+3)}$

Критические точки:

х = 0; х = 3; х = -3

Отметим точки на числовой оси и определим знаки производной на промежутках.

$---(-3)+++[0]---(3)+++$

• Если "+" - функция возрастает, если "-" - функция убывает.

Так данная функция определена на промежутках (-∞; -3) ∪ (3; +∞),

то функция убывает на промежутке  (-∞; -3);

возрастает на промежутке  (3; +∞).

Точек экстремумов нет.

2) Найдем производную второго порядка:

$\displaystyle y'' = \frac{2\cdot(x^2-9)-2x\cdot 2x}{(x^2-9)^2} =\frac{2x^2-18-4x^2}{(x^2-9)^2} =\\\\=\frac{-2x^2-18}{(x^2-9)^2} =\frac{-2(x^2+9)}{(x^2-9)^2}$

y'' < 0 при любом значении х кроме ±3.

$---(-3)---(+3)---$

• Если производная второго порядка положительна, функция вогнута, если отрицательна - выпукла.

⇒ функция выпукла на промежутках (-∞; -3), (3; +∞).

Точек перегиба нет.