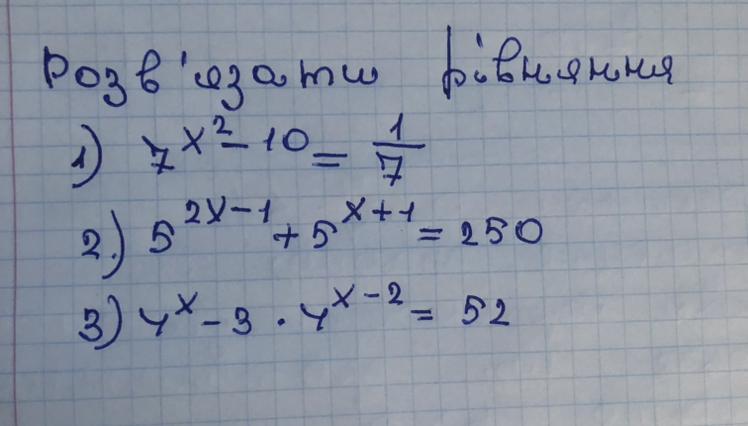Ответы
Ответ дал:
1
Ответ:
Показательные уравнения .
1) Приводим левую и правую части уравнения к показательным функциям с одинаковым основанием .
Приводим уравнение к квадратному относительно .
Проводим обратную замену .
Приложения:

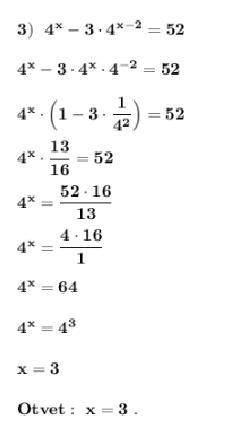
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад