Question

Люди помогите решить эти 2 задания пожалуйста дам 15 баллов

Answer 1

Ответ:

5. $\displaystyle R:r=\sqrt{2}:1$

6. $\displaystyle S(ABC) =\frac{h_1h_2}{2sin\;\beta }$

Объяснение:

5. Вокруг правильного четырехугольника описана окружность и в четырехугольник вписана окружность. Найдите отношение радиусов этих окружностей, если длина меньшей окружности равна 8π.

6. В треугольнике АВС проведены высоты АН и CN, которые соответственно равны h₁ и h₂. Найдите площадь треугольника АВС, если ∠B = β.

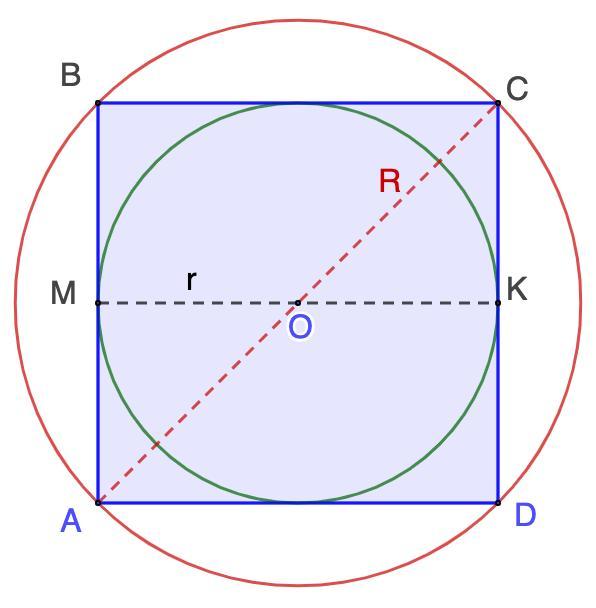
5. Дано: ABCD - квадрат;

Окр.(О;r) - вписана в ABCD;

Окр.(О; R) - описана около ABCD

С вп = 8π

Найти: R : r

Решение:

• Правильный четырехугольник - квадрат.

• Формула длины окружности:

            C = 2πR,

где R - радиус окружности.

C впис. = 2πr

8π = 2πr   ⇒  r = 4

• Диаметр равен двум радиусам.

d = 8

• Диаметр окружности, вписанной в квадрат, равен его стороне.

⇒ АВ = d = 8

• Диаметр окружности, описанной около квадрата, равен его диагонали.

Из ΔАВС по теореме Пифагора найдем АС:

АС² = 64 + 64 = 128   ⇒   AC = 8√2

⇒ R = 4√2

$\displaystyle \frac{R}{r}=\frac{4\sqrt{2} }{4} =\sqrt{2}:1$

6. Дано: ΔАВС;

АН = h₁;   BN = h₂ - высоты;

∠В = β

Найти: S(ABC)

Решение:

Рассмотрим ΔАВН - прямоугольный.

• Синус угла - отношение противолежащего катета к гипотенузе.

$\displaystyle sin\;\beta = \frac{AH}{AB} \\\\AB=\frac{AH}{sin\;\beta }=\frac{h_1}{sin\;\beta }$

• Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне.

$\displaystyle S(ABC) = \frac{1}{2}\cdot AB\cdot CN = \frac{1}{2}\cdot \frac{h_1}{sin\;\beta } \cdot h_2=\frac{h_1h_2}{2sin\;\beta }$

#SPJ1