Question

В правильную квадратную пирамиду вписан куб. Высота пирамиды = 6√2, а сторона основания пирамиды равна 4√2. Найди грань куба. (Даю 100 балла)

Answer 1

Відповідь:

2,4*√2 - ребро куба

Пояснення:

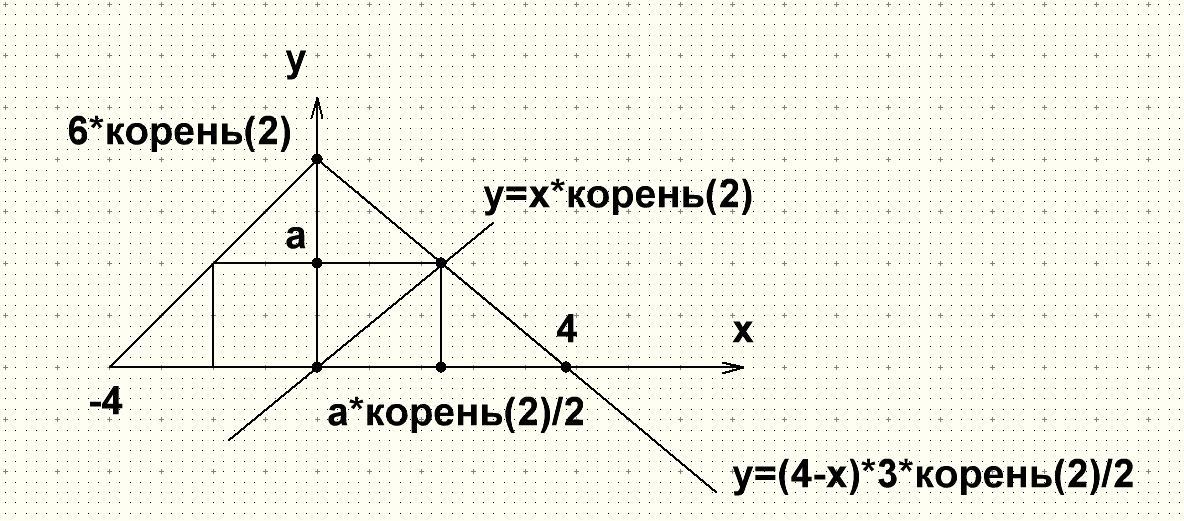
по диагонали основания пирамиды и ее высоте строим сечение
пирамида в сечении отобразится в треугольник с высотой 6√2 и основанием 4√2*√2 = 8
куб в сечении отобразится на прямоугольник высотой а и основанием a√2
уравнение стороны треугольника
у=(4-x)*6√2/4 = (х-4)*3√2/2
уравнение диагонали куба
у = х*√2
решаем
у = (4-x)*3√2/2
у = х*√2

***************
(4-x)*3√2/2=х*√2
у = х*√2

***************
(4-x)*3=х*2
у = х*√2

***************
x=12/5
у = х*√2=12*√2/5 = 2,4*√2 - высота равна длине ребра куба