Question

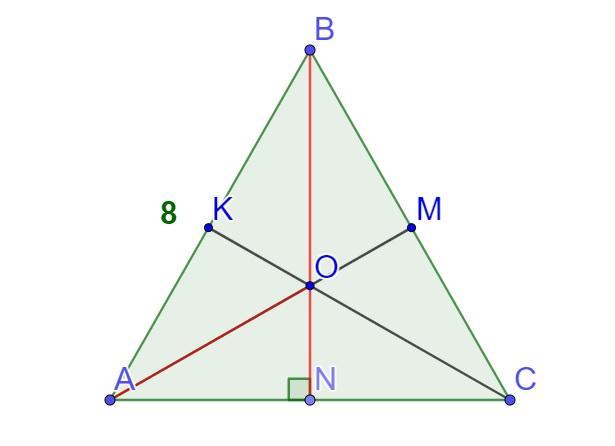
Треугольник ABC равносторонний AM,BN,CK-медианы
O-точка пересечения медиан
AB=8 см найти BN и AO
Даю 25 баллов

Answer 1

Ответ:

ВN = 4√3 см, АО = $\dfrac{8\sqrt{3} }{3}$ см

Объяснение:

Треугольник ABC равносторонний AM,BN,CK-медианы. O-точка пересечения медиан. AB=8 см.  Найти BN и AO.

Дано: ΔАВС, AM,BN,CK-медианы, AM∩BN∩CK=О, AB=8 см

Найти: BN и AO

Решение:

1) В равностороннем треугольнике все стороны равны:

АВ=ВС=АС=8 см.

2) Так как у  равностороннего треугольника медиана, биссектриса и высота, проведенные к основанию треугольника, совпадают, то медиана BN  является также высотой. BN ⊥АС, следовательно ΔАBN - прямоугольный.

3) В прямоугольном ΔАBN (∠АBN =90°) по теореме Пифагора найдём катет BN.

BN² = АВ² - АN²

По условию АВ = 8 см, АN = NС = АС : 2 = 8 : 2 = 4 (см) - по определению медианы Δ.

Тогда: BN² = 8² - 4² = 64 - 16 = 48

ВN = 4√3 см.

4) В равностороннем треугольнике медианы, проведенные к основанию треугольника, равны между собой.

АМ = СК = ВN = 4√3 (см).

5) Точкой пересечения медиан треугольника каждая медиана делится в отношении 2:1.

АО : ОМ = 2 : 1

То есть длина отрезка медианы от вершины треугольника до точки пересечения медиан составляет 2/3 всей ее длины:

$AO = \dfrac{2}{3}\cdot AM = \dfrac{2}{3}\cdot 4\sqrt{3} =\dfrac{8\sqrt{3} }{3}$  (см)

Ответ: ВN = 4√3 см, АО = $\dfrac{8\sqrt{3} }{3}$ см

#SPJ1