Question

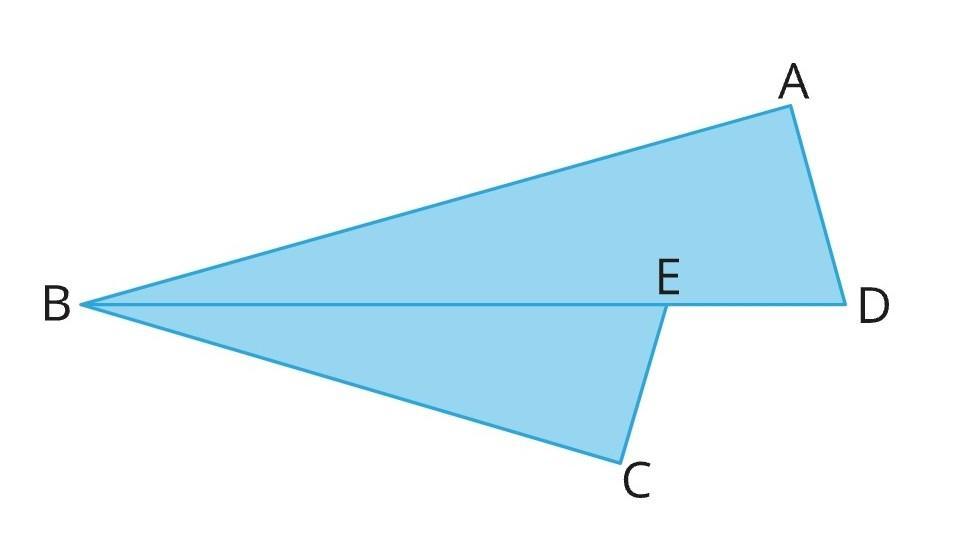
Учитывая, что \(BD\) является биссектрисой угла BD - угла CBA, а также AB⊥AD иBC⊥EC.
Вычислите \(BE\), если \(AD = 9\) \(см\), \(AB = 12\) \(см\), \(EC = 1,8\) \(см\).BE, если AD = 9 см, AB = 12 см, EC = 1,8 см.

Сначала докажите сходство!
Запишите по одной букве или цифре в каждую клетку!

∢A=∢
=
°∢C
D=DBA}⇒ΔEBC∼ΔDBA, после знака l l.

BD=
\(см\)см
BE=
\(см\)см​

Answer 1

Ответ:

2,4 cм

Пошаговое объяснение:

<A = <C= 90

<CBE=<DBA

EC/AD=CB/BA

CB =1,8 *12/9=2,4(cм)

Answer 2

Давайте начнем с доказательства сходства треугольников. Мы имеем:

B
D
BD - биссектриса угла
B
D
A
BDA.
A
B
⊥
A
D
AB⊥AD (перпендикулярны).
B
C
⊥
E
C
BC⊥EC (перпендикулярны).
Из условия 1 и 2 можно сказать, что треугольники
D
B
A
DBA и
D
B
C
DBC подобны (по признаку
L
L
LL). Теперь давайте заполним таблицу:

∢A = ∢C (по свойству биссектрисы)
∢B = ∢B (общий угол)
∢D = ∢D (общий угол)

Теперь, учитывая сходство треугольников
D
B
A
DBA и
D
B
C
DBC, мы можем использовать пропорциональность и отношение сторон:

B
D
D
B
A
=
B
C
D
B
C
DBA
BD
​
=
DBC
BC
​


Значения, которые мы знаем:

A
D
=
9
AD=9 см,
A
B
=
12
AB=12 см,
E
C
=
1.8
EC=1.8 см.

Из этого мы можем выразить
B
D
BD (пусть
B
E
=
x
BE=x):

B
D
=
A
B
−
A
D
=
12
−
9
=
3
BD=AB−AD=12−9=3 см

Теперь мы можем записать пропорцию:

3
x
=
B
C
E
C
x
3
​
=
EC
BC
​


Подставляем известные значения:

3
x
=
B
C
1.8
x
3
​
=
1.8
BC
​


Теперь решим для
x
x:

x
=
3
⋅
1.8
B
C
x=
BC
3⋅1.8
​


Теперь нам нужно найти значение
B
C
BC. Из сходства треугольников
D
B
A
DBA и
D
B
C
DBC мы знаем:

B
C
A
B
=
B
D
A
D
AB
BC
​
=
AD
BD
​


B
C
12
=
3
9
12
BC
​
=
9
3
​


Теперь решим для
B
C
BC:

B
C
=
3
9
⋅
12
=
4
BC=
9
3
​
⋅12=4 см

Теперь можем вычислить
x
x:

x
=
3
⋅
1.8
4
=
1.35
x=
4
3⋅1.8
​
=1.35 см

Итак,
B
E
=
1.35
BE=1.35 см.