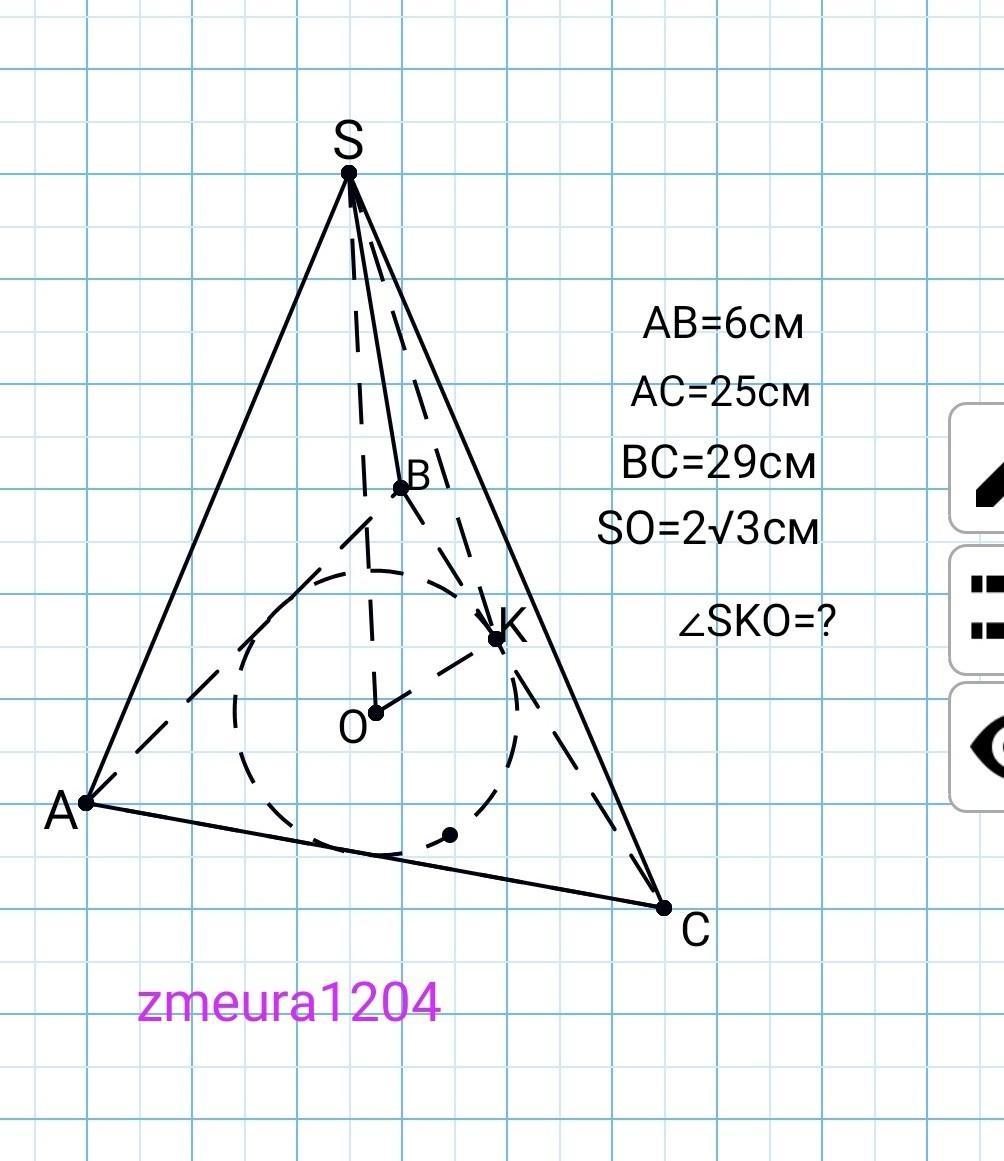
Основою піраміди є трикутник зі сторонами 6 см, 25 см і 29 см. Усі бічні грані однаково нахилені до основи піраміди. Який кут утворюють бічні грані з основою, якщо висота піраміди дорівнює 2√3 см?
Аноним:
напишіть свій інст, там допоможу з вирішенням
У мене немає інстаграму
а тг?
Теж немає
1) За Героном знайти площу.
2) знайти радіус вписаного кола r=S∆/p
3) можна виразити кут через тангенс tg=h/r
Ответы
Ответ дал:
2
Ответ:
Кут нахилу бічної грані до основи дорівнює 60°
Объяснение:
S(∆ABC)=√(p(p-AC)(p-BC)(p-AB));
p=(AB+BC+AC)/2=(6+25+29)/2=30см.
S(∆ABC)=√(30(30-6)(30-25)(30-29))=
=√(30*24*5*1)=√3600=60см²
r=OK;
r=S(∆ABC)/p=60/30=2см.
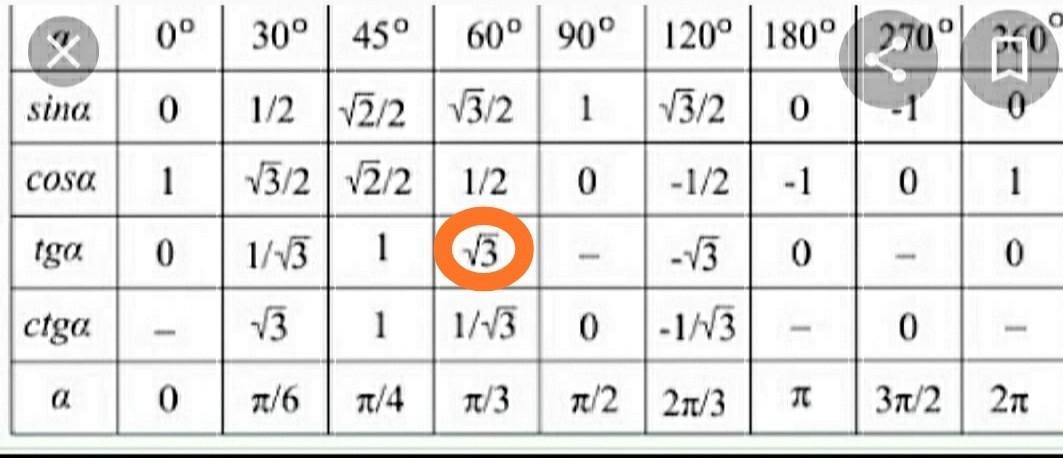
tg∠SKO=SO/OK=2√3/2=√3
∠SKO=arctg√3=60°
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад