Ответы
Ответ:
Для решения данного уравнения, можно воспользоваться свойством степеней, согласно которому a^m = b^m , где a и b - положительные числа (a ≠ 0, b ≠ 0), а m - произвольное действительное число, степень с обоих сторон равна значению в основании.
В данном случае, у нас имеется уравнение:
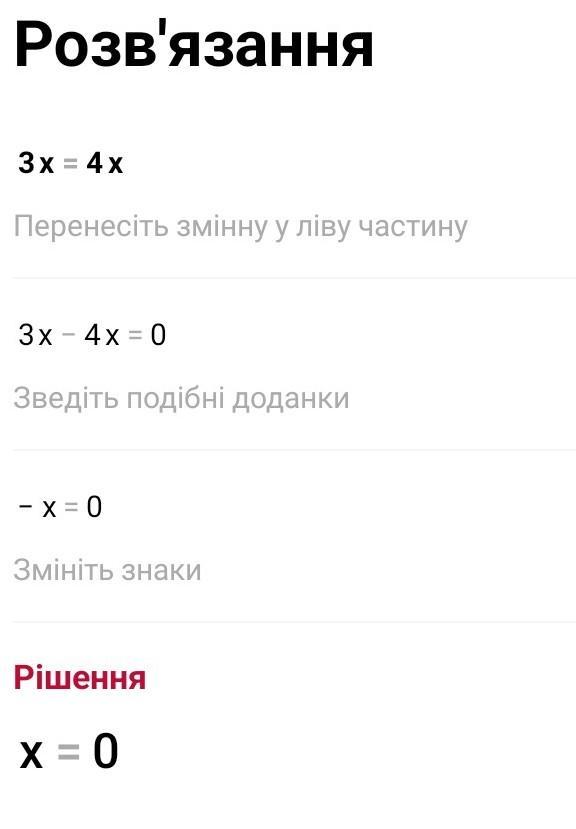
3^x = 4^x
Мы знаем, что 4 = 2^2 , поэтому мы можем выразить 4 в виде степени числа 2:
3^x = (2^2)^x
Затем, принимая во внимание свойство степеней, умножим показатели степени:
3^x = 2^(2x)
Теперь оба основания степеней одинаковые, поэтому показатели степени должны быть равны:
x = 2x
Теперь решим это уравнение относительно x:
x - 2x = 0
- x = 0
Отсюда мы можем сделать вывод, что x = 0.
Итак, решением уравнения 3^x = 4^x является x = 0.
я не впевнена , але по суті має бути правильно