Ответы
Ответ дал:
1
Ответ:
Пошаговое объяснение:
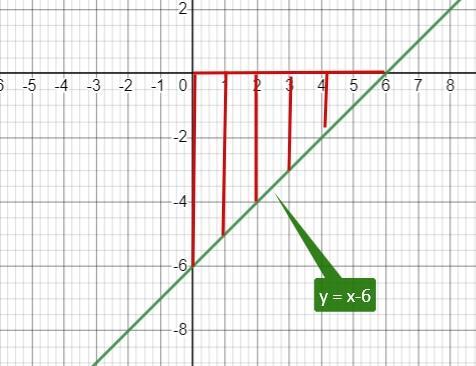
Найдем точки пересечения y = x - 6 с осями координат
ось ординат (х=0)
у = 0 - 6 = (-6)
ось абсцисс (у=0)
0 = х - 6; х = 6.
Таким образом мы имеем равнобедренный прямоугольный треугольник с катетами 6 и 6.
Тогда его площадь равна
Можно, конечно, и через интеграл....
Просто я не знаю, как нужно
линии ограничения
x=0; y₀=0; y₁ = (x-6);
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
8 лет назад